МЕТОД МЦС

Так как точка В принадлежит звену , совершающему вращательное движение, то .

Зная направление скоростей и , находим МЦС звена АВ - , как точку пересечения перпендикуляров, проведенных к и из точек А и В (рис.9).

Скорость находим из отношения

,

 

где и - расстояния до МЦС, измеренные по схеме механизма и переведенные с учетом масштаба в натуральную величину.

Откуда

.

Угловая скорость звена АВ

.

 

Направление угловой скорости звена определяется по направлению скорости вокруг МЦС – в нашем случае против хода часовой стрелки.

Угловая скорость равна:

 

.

 

Так как точка С принадлежит звену АВ, то ее скорость определяется из отношения:

 

 

Вектор 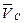направляем перпендикулярно отрезку в сторону вращения звена АВ. Затем находим МЦС звена CDE - и аналогично определяем скорости и угловые скорости , и

 

 

Рис..9. Метод определения скоростей с помощью МЦС

 

 

 

 

МЕТОД ПЛАНОВ СКОРОСТЕЙ.

 

Определяем скорость точки А:

и из произвольно выбранного полюса 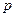откладываем отрезок который в масштабе ,

 

представляет скорость (рис 11).

 

 

Рис. 10.

 

Затем переходим к рассмотрению движения звена АВ, совершающего плоское движение. Используем теорему о распределении скоростей

 

,

где

.

 

В соответствии с векторным уравнением, из точки проводим линию перпендикулярную АВ, а из полюса скоростей 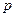- линию перпендикулярную . Точка пересечения этих линий определяет скорость точки В. Измеряя длины отрезков, с помощью масштабного коэффициента, находим

 

Используя соотношение ,

 

находим

 

 

 

Рис.11. План скоростей механизма.

 

Вектор 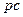на плане указывает направление скорости .

Далее рассмотрим движение звена CDE. Составляем уравнение для определения скорости точки D

 

где

и из последующего построения плана скоростей находим

 

 

Для определения составляем систему уравнений:

 

 

в соответствии, с которым строим план скоростей для точки и находим

 

.

 

Составляя уравнение

 

завершаем построение плана скоростей механизма, по которому находим

 

 

Результаты расчетов сводим в таблицу 1.

Таблица 1

Способ определения	Скорости точек, см/с
VA	VB	VC	VD	VE	VF
По плану скоростей	0,6	0,67	0,57	0,21	0,33	0,26
С помощью МЦС	0,6	0,67	0,58	0,2	0,33	0,26
Способ определения	Угловые скорости звеньев, рад/с
По плану скоростей		0,43	0,45	0,24	1,34	0,38
С помощью МЦС		0,43	0,45	0,24	1,34	0,37

 

Несущественные расхождения результатов объясняются погрешностью построения.

 

ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ

 

Построение начинаем с определения ускорения точки А. Так как кривошип OA вращается равномерно, то

Из произвольно выбранного полюса откладываем отрезок , который в масштабе

 

 

представляет ускорение точки А (рис.12).

Для определения ускорения точки В применим теорему о распределении ускорений для звена АВ.

Так как точка В принадлежит также звену , то

 

 

Таким образом, векторное уравнение для определения ускорения точки В примет вид

 

 

где

 

 

 

Построение проводим в следующей последовательности. Из точки отрезка откладываем отрезок

 

 

представляющий собой ускорение

Из точки проводим прямую, перпендикулярную к АВ, вдоль которой направлено ускорение

Из полюса плана ускорений откладываем отрезок представляющий собой ускорение

 

,

 

а из точки проводим прямую, перпендикулярную , до пересечения с прямой перпендикулярной АВ. Точка пересечения этих перпендикуляров определяет точку

Измеряя длины отрезков, с учетом масштаба построения, находим:

 

Определяем угловые ускорения звеньев

 

 

Для определения направления углового ускорения звена АВ вектор касательного ускорения переносится с плана ускорения в точку В звена. По направлению вращения с вокруг точки А определяем направление .

 

 

Рис.12. Построение плана ускорений.

Из подобия отрезков определяем , а затем находим ускорение точки С

 

 

Для определения ускорения точки D составляем уравнение

 

 

где

 

Из построений находим

 

 

Ускорение точки E находим из системы уравнений:

где

 

Из построения находим точку С. При этом  .

Ускорение точки С

 

 

В заключении, определяем ускорение точки F, составляя уравнение

 

 

где

 

Из построений находим точку плана ускорений и величины ускорений

 

 

Направления угловых ускорений звеньев указываем на плане механизма. Значения ускорений звеньев сводим в таблицу 2.

 

Таблица 2

 

Ускорения точек, м/с2	Угловые ускорения звеньев, с-2
0,61	1,07	0,89	1,2	0,28	0,92	0,3	1,2	0,5	2,2	0,6

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Какое движение твердого тела считается плоским? Каковы уравнения плоского движения?

2. На какие движения можно разложить плоскопараллельное движение твердого тела?

3. Как изменяются уравнения плоского движения твердого тела при перемене полюса?

4. Как определяется угловая скорость и угловое ускорение плоской фигуры, если известны уравнения плоского движения тела?

5. Что называется мгновенным центром скоростей плоской фигуры?

6. Как определяется положение мгновенного центра скоростей плоской фигуры?

7. Как определяются скорости точек тела при плоском движении с помощью МЦС?

8. Как определяется угловая скорость тела при плоском движении с помощью МЦС?

9. Что называется планом скоростей?

10. На основании какой теоремы строится план скоростей?

11. Что представляет собой отрезок, соединяющий две вершины плана скоростей?

12. Как определяется угловая скорость тела с помощью плана скоростей?

13. Что называется планом ускорений механизма?

14. Сформулируйте теорему о распределении ускорений точек тела при плоском движении.

15. Как определяется угловое ускорение тела с помощью плана ускорений?

16. Как определяется положение мгновенного центра ускорений плоской фигуры?

17. Как определяется ускорение точек плоской фигуры с помощью МЦУ?