Задача минимизации времени выполнения проекта.
Минимизация времени выполнения проекта возможна только за счет сокращения продолжительности выполнения работ, лежащих на критическом пути L 
. При этом стоимость этих работ и всего проекта увеличится согласно соотношениям (3.1) и (3.6). для решения этой задачи проводится расчет исходного сетевого графика, а затем выполняется его оптимизация. В начальном сетевом графике продолжительность всех работ может считаться равной максимальному значению (
= 
).Далее выполняются следующие условия:
1. Составляется список всех полных путей ( алгоритм перебора).
2. определяется длительность каждого полного пути.
3. начиная с критических путей, строятся линейные графы всех полных путей с упорядочиванием по убыванию их длительности:
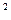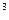>T 
>T 
>…>T 
>T 
Сверху над каждой работой записывается 
а снизу( - 
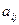)(возможное сокращение ее длительности).
4. Начиная с k=1 на каждом шаге k составляется список всех критических путей 
. Обозначается их длительность через 
, а стоимость сетевого графика обозначается через 
. Если все 
, то расчеты на данном шаге закончены. Переход к 6.
5. для путей списка определяются работы, подлежащие сокращению по двум возможным вариантам 5.1 и 5.2.
Вариант 5.1. есть работы, общие для всех путей . В этом случае выбирается одна общая работа для всех путей в , для которой минимальна величина и продолжительность ее выполнения не равна минимальному сроку:
(3.7.)
Определяется время сокращения длительности выбранной общей работы (p,q) каждом пути по формуле
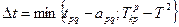(3.8.)
Т.е. сокращение длительности работы не больше ее минимального времени выполнения и не превышает длительности ближайшего к критическому пути 
( шаг 3), не вошедшего в список . Определяется новая продолжительность 
выбранной работы:
= 
- 
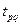(3.9.)
Согласно (3.9.) длительность всех путей , содержание всей работы (p,q) в каждом пути по формуле:
(3.10.)
С учетом изменения времени выполнения работ проводится пересчет длин всех полных путей:
( 
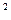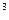>T >T >…>T >T ).
Определяется новая стоимость сетевого графика
(3.11)
Зависимость стоимости сетевого графика от длительности критического пути определяется по формуле:
(3.12.)
Если новая продолжительность = 
, то при решении задач (3.7) исключается работа (p,q), поскольку она не имеет больше резерва снижения.
Увеличиваем шаг на единицу, т.е. полагаем k равным k+1 и осуществляем переход к шагу 4 до тех пор, пока k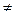 
n. Иначе идем к шагу 6.
Вариант 5.2. в списке нет общих работ. В каждом пути выбирается по одной работе с минимальным значением :
(3.13.)
Список этих работ обозначается через Q= 
. Определяется длительность сокращения выбранных работ по формуле (3.8.) для всего списка Q.
Определяется новая продолжительность выбранных работ по формуле (3.9.) и новое время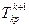 
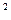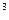для путей по формуле (3.10.). Осуществляется пересчет длин всех полных путей ( >T >T >…>T >T ) с учетом изменения времени выполнения работ. Определяется стоимость сетевого графика:
(3.14.)
Где сумма берется по всем выбранным работам. Зависимость стоимости сетевого графика от длительности критического пути определяется по формуле:
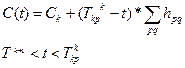(3.15.)
Работы, у которых новая продолжительность = исключаются при решении задачи (3.13.), поскольку они не имеют больше резерва снижения.
Увеличиваем шаг k на 1(k+1) и осуществляем переход к 4 шагу до тех пор, пока k 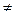n. Иначе идем к шагу 6.
6. На основе формулы (3.12.) и (3.15.) строится график зависимости стоимости сетевого графика от длительности критического пути C=C(t).
7. Для определения минимального времени выполнения заданной стоимости С* проекта решается уравнение виды С(t*)=C*.
Сделаем ряд замечаний к данному алгоритму. Дополнительные затраты, связанные с сокращением времени выполнения проекта с t1 и t2, равны C(t1)-C(t2). Для учета шагов алгоритма следует вести таблицу длительности и стоимости работ и длительности полных путей.
Другим вариантом данного алгоритма является случай, когда начальный сетевой график построен при минимальных сроках выполнения каждой работы, а затем последовательно увеличивают длину критического пути, увеличивая сроки выполнения некритических, а затем и критических работ по критерию максимума коэффициента напряженности .
Пример 4.Провести минимизацию времени выполнения проекта при заданных затратах на его осуществление и построить зависимость стоимости от критического времени C=C(t). Исходные данные задачи в табл. 3.4.
Таблица 3.4.
| № п\п | Работы | Продолжительность работы |
| Стоимость работы при
=
| |
|
|
| ||||
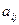
| (0,1) | |||||
| (0,2) | |||||
| (1,2) | |||||
| (1,3) | |||||
| (2,7) | |||||
| (3,4) | |||||
| (3,5) | |||||
| (4,6) | |||||
| (5,6) | |||||
| (6,7) | |||||
| (7,8) | |||||
| Итого |
Находим все полные пути сетевого графика и их длины:
L1: 0 – 1 – 3 – 4 – 6 – 7 – 8, t(L1) = tкр = 99;
L2: 0 – 1 – 3 – 5 – 6 – 7 – 8, t(L2) = 89;
L3: 0 – 1 – 2 – 7 – 8, t(L3) = 50;
L4: 0 – 2 – 7 – 8, t(L4) = 50.
Для удобства дальнейших расчетов представим эти пути графически виде цепочек, в которых цифры над каждой работой показывают коэффициенты затрат на ускорение работы , а под стрелками- максимально возможные величины уменьшения продолжительности работ
= - .
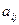Ниже построены схемы всех полных путей:
1. Первоначальная стоимость проекта С = 300. Критическим является путь L2, его длина tкр = 99. Уменьшение продолжительности выполнения комплекса можно только за счёт сокращения продолжительности работ пути L2. Из работ критического пути L2 наименьший коэффициент hij имеет работа (3, 4): h34 = 2. Продолжительность работы (3, 4) можно сократить не более чем на 10 суток. Действительно, ∆t = min{b34 – a34, Tkp -T1} = min{10, 99 – 89} = 10. При этом изменяется длина только критического пути L2 (с 99 до89 суток), единственного пути, проходящего через работу (3, 4). Стоимость всего проекта за счет ускорения работы (3, 4) возрастет на
2⋅10 = 20 единиц и станет равной 300 + 20 = 320.
Итак, согласно (3.15) получаем С(t) = 300 + 2(99 − t),89 ≤ t ≤ 99. Новые длины путей равны t(L1) = t(L2) = 89, t(L3) = t(L4) = 50, tкр = 89.
2. Есть два критических пути L1 и L2 и сократить срок выполнения проекта можно за счет одновременного сокращения их продолжительности, изменяя продолжительность работ, лежащих на этих путях: либо (0, 1), либо (1, 3), либо (6, 7), либо (7, 8). Остановимся на работе (6, 7), поскольку при этом обеспечивается минимум затрат на ускорение. Действительно, из работ критических путей L1 и L2 наименьший коэффициент h67 = 5 имеет работа (6, 7).
Продолжительность работы (6,7) можно уменьшить не более чем на 5 дней. Действительно , ∆t =min{b67 – a67, Tkp – T2} = min{5, 89 – 50} = 5. На эту величину уменьшатся длины критических путей t(L1) и t(L2), а следовательно, и срок выполнения проекта. При этом стоимость работы (6, 7) возрастет на 5*5 = 25 усл. единиц, а для всего проекта она увеличится с 320 до 345 усл.ед. Согласно (3.15), получаем С(t) = 320 + 5(89 − t),84 ≤ t ≤ 89.
3. С = 345; t(L2) = t(L1) = 84; t(L3) = t(L4) = 50; tкр = 84. Критическими являются пути L1 и L2, tкр = 84, = {L1, L2 }. Из работ на критических путях L1 и L2 наименьший коэффициент имеет работа (0, 1): h01 = 6.
Действительно, hmin(i, j) = min(h(0, 1), h(1, 3), h(7, 8)) = min(6, 8, 9) = 6.
Продолжительность общей работы (0, 1) на этих путях можно сократить на 10 дней: ∆t = min{b01 – a01, Tkp – T2} = min{10, 84 – 50} = 10.
Согласно (3.15) получаем С(t) = 345 + 6(84 − t),74 ≤ t ≤ 84.
Стоимость работы (0, 1) и всего проекта возрастет на 6*10 = 60 единиц,
С01 = 35 + 60 = 95. Новые значения стоимости проекта и длин критических путей: С = 345 + 6⋅10 = 405, t(L1) = t(L2) = 74.
4. С = 405, t(L1) = t(L2) = 74, t(L3) = 40, t(L4) = 50. Критическими являются пути L1 и L2. tкр = 74, = {L1, L2}. hmin(i, j) = min(h(1, 3), h(7, 8)) = min(8, 9) = 8, hmin = h(1, 3) =8. Продолжительность общей работы (1, 3) сокращается на 5 дней:
∆t = min{b13 – a13, Tkp – T2} = min{5, 74–50} = 5.
Согласно (3.15) получаем С(t) = 405 + 8(74 − t),69 ≤ t ≤ 74.
Стоимость работы (1, 3) и всего проекта возрастет на 8*5 = 40 единиц,
С13 = 10 + 40 = 50. Новое значение С = 405 + 8⋅5 = 445, t(L1) = t(L2) = 69.
5. С = 445, t(L1) = t(L2) = 69, t(L3) = 40, t(L4) = 50. Критическим являются
пути L1 и L2. tкр = 69, = {L1, L2}. hmin(i, j) = h(7, 8) = 9. Продолжительность общей работы (7, 8) сокращается на 5 дней:
∆t = min{b78 – a78, Tkp – T2} = min{5, 69–50} = 5.
Согласно (3.15) получаем С(t) = 445 + 9(69 − t),64 ≤ t ≤ 69.
Стоимость работы (7, 8) и всего проекта возрастет на 9*5 = 45 единиц,
С78 = 20 + 45 = 65. Новое значение С = 445 + 9⋅5 = 490, t(L1) =t(L2) = 64.
6. С = 490, t(L1) = t(L2) = 64, t(L3) = 35, t(L4) = 45. Критическими являются пути L1 и L2, tкр = 64, = {L1, L2}. Общих работ на этих путях нет. Можно сократить работы (3,5) и (5,6) пути L1 на 5 дней и работу (4, 6) пути L2 на 10 дней. Одновременно можно сократить на 5 дней продолжительность работы (5, 6) пути L1 и работы (4, 6) пути L2.
Действительно, ∆t = min{b46 – a46, b56 – a56, Tkp – T2} = min{10, 5, 64 – 50} = 5. Коэффициенты напряженности этих работ равны соответственно h(5, 6) = 4, h(4, 6) = 4. Коэффициент затрат на ускорение работ равен h(5, 6) + h(4, 6) = 4 + 4 = 8.
Согласно (3.15) получаем С(t) = 490 + 8(64 − t),59 ≤ t ≤ 64.
Стоимость работы (4, 6) возрастет на 4*5 = 20, а работы (5, 6) на 4*5 = 20 единиц: С46 = 40 + 20 = 60, С56 = 30 + 20 = 50.
Новые значения С = 490 + 8*5 = 530, t(L1) = t(L2) = 59.
7. С = 530, t(L1) = t(L2) = 59, t(L3) = 35, t(L4) = 45.
Критическими являются пути L1 и L2. tкр = 59, = {L1, L2 }.
Общих работ нет. Теперь можно одновременно сократить на 5 дней продолжительность работы (3, 5) пути L1 и работы (4, 6) пути L2:
∆t = min{b35 – a35, b46 – a46 , Tkp – T2} = min{5, 5, 59–50} = 5.
Коэффициенты напряженности этих работ равны h(3, 5) = 6, h(4, 6) = 4 соответственно. Коэффициент затрат на ускорение обеих работ будет равен h(3, 5) + h(4, 6) = 6 + 4 = 10.
Следовательно: С(t) = 530 + 10(59 − t),54 ≤ t ≤ 59.
Стоимость работы (3,5) возрастет на 6*5 = 30, а работы (4, 6) – на 4*5 = 20
единиц: С35 = 15 + 30 = 45, С46 = 60 + 20 = 80.
Новые значения С = 530 + 105 = 580, t(L1) = t(L2) = 54.
Алгоритм продолжается до тех пор, пока есть tij> aij.
Шаги алгоритма представим в табл. 3.5.
Таблица длительности стоимости работ.
Таблица 3.5
| № п\п | Работа | Шаг алгоритма | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | (0,1) | 20/35 | 10/95 | |||||
| 2 | (0,2) | 32/50 | ||||||
| 3 | (1,2) | 12/15 | ||||||
| 4 | (1,3) | 7/10 | 2/50 | |||||
| 5 | (2,7) | 7/10 | ||||||
| 6 | (3,4) | 26/50 | 16/70 | |||||
| 7 | (3,5) | 13/15 | ||||||
| 8 | (4,6) | 22/40 | 17/60 | |||||
| 9 | (5,6) | 25/30 | 20/50 | |||||
| 10 | (6,7) | 13/25 | ||||||
| 11 | (7,8) | 11/20 | 6/65 | |||||
| Стоимость проекта | 300 | 320 | 345 | 405 | 445 | 490 | 530 |
Ниже представлены длительности полных путей на различных шагах алгоритма (табл. 3.6.)
Таблица длительности полных путей.
Таблица 3.6
| Длительность полных путей | Шаг алгоритма | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| T(L1) | 99 | 89 | 84 | 74 | 69 | 64 | 59 | |
| T(L2) | 89 | 89 | 84 | 74 | 69 | 64 | 59 | |
| T(L3) | 50 | 50 | 50 | 40 | 40 | 35 | 35 | |
| T(L4) | 50 | 50 | 50 | 50 | 50 | 45 | 45 | |
Теперь, построив функцию С(t), можно определить время выполнения проекта t* для любых затрат С* и наоборот.
Например, из шага 3 следует, что при стоимости проекта С* = 375 усл. р. минимальная продолжительность проекта будет равна t* = 79 дней, а из шага 7 видно, что при стоимости С* = 540 усл. р. t* = 55 дней.
С помощью функции С(t) можно оценить и дополнительные затраты, связанные с сокращением сроков завершения проекта. Так, сокращение продолжительности проекта с 79 до 55 дней потребует дополнительно 540 – 375 = 165 усл. р.
В заключение сделаем следующее замечание. При линейной зависимости стоимости работ от их продолжительности задача оптимизации сетевого графика может быть поставлена в виде задачи линейного программирования, в которой необходимо минимизировать стоимость проекта при двух группах ограничений. Первая группа ограничений - ограничения на время выполнения работ, вторая группа ограничений показывает, что продолжительность всех полных путей не должна превышать заданного времени выполнения проекта. Однако решать такие задачи линейного программирования классическими методами неэффективно.<олжна превышать заданного времени выполнения проекта. Однако решать такие задачи линейного программирования классическими методами неэффективно.