Как найти асимптоты графика функции?
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:
Пример 1
Найти асимптоты графика функции
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при 
, и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статьеНепрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем 
. В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число:
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАКрасположен график функции и построить егоКОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:
Вывод: односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при 
.
2) Проверим наличие наклонных асимптот:
Первый предел конечен, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен.
Таким образом, наша асимптота:
Вывод: прямая, заданная уравнением 
является горизонтальной асимптотой графика функции при 
.
Для нахождения горизонтальной асимптоты
можно пользоваться упрощенной формулой:
Если существует конечный предел 
, то прямая 
является горизонтальной асимптотой графика функции 
при 
.
Нетрудно заметить, что числитель и знаменатель функции 
одного порядка роста, а значит, искомый предел будет конечным:
Ответ: 
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов 
, попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение: Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде 
Найдём односторонние пределы в точке 
:
И в точке 
:
Таким образом, прямые 
являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию 
, то совершенно очевидно, что предел 
будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая 
(ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ: 
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка – в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4порядок роста знаменателя больше, чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста. В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая – через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение: классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен, поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:
Второй предел тоже конечен, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод: 
Таким образом, при график функции бесконечно близко приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку 
.
Прямая является вертикальной асимптотой для графика 
при 
.
2) Наклонные асимптоты:
Прямая 
является наклонной асимптотой для графика при .
Ответ: 
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, 
).
Но в жизни происходят и другие чудеса:
Пример 9
Исследовать график функции на наличие асимптот
Решение: функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:
Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:
Строго говоря, здесь две неопределённости: 
и 
, но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности. Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой 
:
Ответ: 
Пожалуй, самая популярная наклонная асимптота.
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты 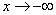при 
и при 
:
Пример 10
Исследовать график функции на наличие асимптот
Решение: подкоренное выражение положительно, значит, область определения – любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс» стремится к «минус бесконечности», то: 
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:
Таким образом, прямая 
является наклонной асимптотой графика при .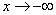
С «плюс бесконечностью» всё тривиальнее:
А прямая 
– при .
Ответ:
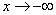, если ;
, если .
Не удержусь от графического изображения:
Это одна из ветвей гиперболы 
.
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции:
Пример 11
Исследовать график функции на наличие асимптот
Решение: очевидно, что 
, поэтому рассматриваем только правую полуплоскость, где есть график функции.
1) Функция непрерывна на интервале 
, а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки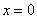 
справа:
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов).
Таким образом, прямая 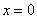(ось ординат) является вертикальной асимптотой для графика функции при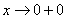 
.
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статьеПравила Лопиталя мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: 
(см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ:
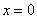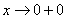, если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции 
асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции, а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Пример 13
Исследовать график функции на наличие асимптот
А здесь могут быть только наклонные асимптоты, причём направления 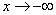, следует рассмотреть отдельно.
Надеюсь, вы отыскали нужную асимптоту =)
Желаю успехов!
Решения и ответы:
Пример 2:Решение:
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке 
. Найдём односторонние пределы:
Прямая является вертикальной асимптотой графика функции при 
.
2) Наклонные асимптоты.
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ: 
Чертёжк Примеру 3:
Пример 4:Решение:
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке 
. Вычислим односторонние пределы:
Примечание: бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу: 
.
Прямая является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ: 
Пример 5:Решение:
1) Исследуем функцию на наличие вертикальных асимптот. Найдём точки, в которых знаменатель обращается в ноль:
Действительных корней нет.
Исследуемая функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствуют.
2) Наклонные асимптоты.
Прямая 
является горизонтальной асимптотой графика функции при .
Ответ:
Чертёжк Примеру 7:
Пример 8: Решение:
1) Вертикальные асимптоты. Исследуем точку .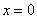
,
Примечание: бесконечно малое отрицательное число в нечётной степени равно бесконечно малому отрицательному числу: 
.
.
Прямая 
(ось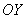 
) является вертикальной асимптотой для графика , если 
.
2) Наклонные асимптоты:
Прямая 
является наклонной асимптотой для графика при .
Ответ: 
График данной функции:
Пример 12:Решение: найдёмобласть определения функции:
.
Помимо аналитического способа нахождения области определения можно использовать иметод интервалов.
1) Проверим наличие вертикальных асимптот. Для удобства и наглядности вычислений разложим аргумент логарифма на множители:
Вычислим односторонние пределы:
Таким образом, прямые 
являются вертикальными асимптотами для графика функции при 
и 
соответственно.
2) Наклонные асимптоты.
Дважды используемправило Лопиталя:
Первый предел конечен, находим второй предел:
Значит, наклонные асимптоты отсутствуют.
Ответ:
, если ;
, если .
Пример 13:Решение: так как функция непрерывна на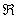 
, то вертикальные асимптоты отсутствуют.
Выясним, есть ли у графика наклонные асимптоты:
Значит, при 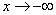у графика нет наклонной асимптоты.
Таким образом, прямая является горизонтальной асимптотой графика данной функции при .
Ответ: ось абсцисс при .
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Нули функции. Интервалы знакопостоянства функции.
Метод интервалов
Значительная доля материала, касающегося производных и исследования функций, традиционно относится к школьной программе, и данная статья не является исключением из правила. Сегодня мы потренируемся в нахождении нулей и интервалов знакопостоянства функции, а также подробно разберём метод интервалов, который можно сравнить с надёжной арматурой в стенах рассматриваемой темы. Если же проект вашего здания находится на стадии котлована, пожалуйста, начните с вводного урокао графиках функций. Кроме того, желательно ознакомиться со статьями Область определения функции,Асимптоты графика, и, по существу, информация этой странички – логическое продолжение. Материал, естественно, будет полезен и старшеклассникам.
Открываем карты: