Область определения функции с логарифмом
Третья распространённая функция – логарифм. В качестве образца я буду рисовать натуральный логарифм, который попадается примерно в 99 примерах из 100. Если некоторая функция содержит логарифм  , то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству
, то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству  . Если логарифм находится в знаменателе:
. Если логарифм находится в знаменателе:  , то дополнительно накладывается условие
, то дополнительно накладывается условие  (так как
(так как  ).
).
Пример 9
Найти область определения функции

Решение: в соответствии с вышесказанным составим и решим систему:

Графическое решение для чайников:

Ответ: область определения: 
Остановлюсь ещё на одном техническом моменте – у меня ведь не указан масштаб и не проставлены деления по оси. Возникает вопрос: как выполнять подобные чертежи в тетради на клетчатой бумаге? Отмерять ли расстояние между точками по клеточкам строго по масштабу? Каноничнее и строже, конечно, масштабировать, но вполне допустим и схематический чертёж, принципиально отражающий ситуацию.
Пример 10
Найти область определения функции

Для решения задачи можно использовать метод предыдущего параграфа – проанализировать, как парабола расположена относительно оси абсцисс. Ответ в конце урока.
Как видите, в царстве логарифмов всё очень похоже на ситуацию с квадратным корнем: функция  (квадратный трёхчлен из Примера №7) определена на интервалах
(квадратный трёхчлен из Примера №7) определена на интервалах  , а функция
, а функция  (квадратный двучлен из Примера №6) на интервале
(квадратный двучлен из Примера №6) на интервале  . Неловко уже и говорить, функции типа
. Неловко уже и говорить, функции типа  определены на всей числовой прямой.
определены на всей числовой прямой.
Полезная информация: интересна типовая функция  , она определена на всей числовой прямой кроме точки
, она определена на всей числовой прямой кроме точки 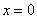 . Согласно свойству логарифма
. Согласно свойству логарифма  , «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» необходимо заключить под знак модуля:
, «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» необходимо заключить под знак модуля:  . Вот вам и ещё одно «практическое применение» модуля = ). Так необходимо поступать в большинстве случаев, когда вы снОсите чётную степень, например:
. Вот вам и ещё одно «практическое применение» модуля = ). Так необходимо поступать в большинстве случаев, когда вы снОсите чётную степень, например:  . Если же основание степени заведомо положительно, например,
. Если же основание степени заведомо положительно, например,  , то в знаке модуля отпадает необходимость и достаточно обойтись круглыми скобками:
, то в знаке модуля отпадает необходимость и достаточно обойтись круглыми скобками:  .
.
Чтобы не повторяться, давайте усложним задание:
Пример 11
Найти область определения функции

Решение: в данной функции у нас присутствует и корень и логарифм.
Подкоренное выражение должно быть неотрицательным:  , а выражение под знаком логарифма – строго положительным:
, а выражение под знаком логарифма – строго положительным:  . Таким образом, необходимо решить систему:
. Таким образом, необходимо решить систему:

Многие из вас прекрасно знают или интуитивно догадываются, что решение системы должно удовлетворять каждому условию.
Исследуя расположение параболы  относительно оси
относительно оси 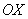 , приходим к выводу, что неравенству
, приходим к выводу, что неравенству  удовлетворяет интервал
удовлетворяет интервал  (синяя штриховка):
(синяя штриховка):

Неравенству  , очевидно, соответствует «красный» полуинтервал
, очевидно, соответствует «красный» полуинтервал  .
.
Поскольку оба условия должны выполняться одновременно, то решением системы является пересечение данных интервалов. «Общие интересы» соблюдены на полуинтервале  .
.
Ответ: область определения: 
Типовое неравенство  , как демонстрировалось в Примере №8, нетрудно разрешить и аналитически.
, как демонстрировалось в Примере №8, нетрудно разрешить и аналитически.
Найденная область определения не изменится для «похожих функций», например, для  или
или  . Также можно добавить какие-нибудь непрерывные на
. Также можно добавить какие-нибудь непрерывные на  функции, например:
функции, например:  , или так:
, или так:  , или даже так:
, или даже так:  . Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится (хотя в общем случае это не всегда справедливо). Ну а в теории матана по поводу этого словесного… ой… существуют теоремы.
. Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится (хотя в общем случае это не всегда справедливо). Ну а в теории матана по поводу этого словесного… ой… существуют теоремы.
Пример 12
Найти область определения функции

Это пример для самостоятельного решения. Использование чертежа вполне уместно, так как функция не самая простая.
Ещё пару примеров для закрепления материала:
Пример 13
Найти область определения функции

Решение: составим и решим систему:

Все действия уже разобраны по ходу статьи. Изобразим на числовой прямой интервал, соответствующий неравенству  и, согласно второму условию, исключим две точки:
и, согласно второму условию, исключим две точки:

Значение  оказалось вообще не при делах.
оказалось вообще не при делах.
Ответ: область определения 
Небольшой математический каламбур на вариацию 13-го примера:
Пример 14
Найти область определения функции

Это пример для самостоятельного решения. Кто пропустил, тот в пролёте ;-)
Завершающий раздел урока посвящен более редким, но тоже «рабочим» функциям:
Области определения функций
с тангенсами, котангенсами, арксинусами, арккосинусами
Перед изучением параграфа рекомендую вновь вернуться к первой статье о графиках, чтобы освежить визуальную и аналитическую информацию о перечисленных в заголовке функциях.
Если в некоторую функцию входит  , то из её области определения исключаются точки
, то из её области определения исключаются точки  , где Z – множество целых чисел. В частности, как отмечалось в статьеГрафики и свойства элементарных функций, у функции
, где Z – множество целых чисел. В частности, как отмечалось в статьеГрафики и свойства элементарных функций, у функции  выколоты следующие значения:
выколоты следующие значения:

То есть, область определения тангенса:  .
.
Убиваться сильно не будем:
Пример 15
Найти область определения функции

Решение: в данном случае  и в область определения не войдут следующие точки:
и в область определения не войдут следующие точки:

Скинем «двойку» левой части в знаменатель правой части:

В результате  :
:

Ответ: область определения:  .
.
В принципе, ответ можно записать и в виде объединения бесконечного количества интервалов, но конструкция получится весьма громоздкой:

Аналитическое решение полностью согласуется с геометрическим преобразованием графика: если аргумент функции умножить на 2, то её график сожмётся к оси  в два раза. Заметьте, как у функции
в два раза. Заметьте, как у функции  уполовинился период, и точки разрыва участились в два раза. Тахикардия.
уполовинился период, и точки разрыва участились в два раза. Тахикардия.
Похожая история с котангенсом. Если в некоторую функцию входит  , то из её области определения исключаются точки
, то из её области определения исключаются точки  . В частности, для функции
. В частности, для функции  автоматной очередью расстреливаем следующие значения:
автоматной очередью расстреливаем следующие значения:

Иными словами: 
Миниатюра для самостоятельного решения:
Пример 16
Найти область определения функции

Арксинус с арккосинусом, как всегда, выступают хедлайнером математического концерта, и этого стоило дождаться, поскольку кроме нахождения области определения вы сможете научиться решать двойные неравенства (или повторить их).
Если в некоторую функцию входит  или
или  , то на её область определения накладывается ограничение в виде двойного неравенства:
, то на её область определения накладывается ограничение в виде двойного неравенства:  .
.
Пример 17
Найти область определения функции

Решение: составим двойное неравенство:

Действия с двойным неравенством очень похожи на действия с «обычным» одинарным неравенством. Конечная цель преобразований – добиться, чтобы в середине остался только «икс».
Сначала избавимся в средней части от константы, для этого вычтем из каждой части неравенства «тройку»:

Умножим все три части неравенства на –1. Поскольку множитель отрицателен, то знаки самих неравенств необходимо «развернуть» в противоположную сторону:

Умножим все части неравенства на  :
:

Запишем ответ, переставив знаки неравенств в привычном порядке, а то по-арабски как-то получилось – от «единицы» до «двух» справа налево.
Ответ: область определения:  или
или 
Несложный заключительный пример для самостоятельного решения:
Пример 18
Найти область определения функции

Хотелось разобрать более трудные примеры со сложными функциями когда, скажем, под квадратный корень вложена дробь или логарифм, но для этого нужно рассказывать прометод интервалов, который сейчас наверняка запутает значительную часть аудитории. В этой связи я решил перенести объяснения на урок о нулях и интервалах знакопостоянства функции, где постараюсь вернуться к нахождению области определения сложных функций. А на данный момент лучше усвоить меньше, да качественнее!
Желаю успехов!
Решения и ответы:
Пример 2: Область определения: 
Пример 4: Решение: найдём нули знаменателя:

Ответ: область определения: 
Пример 6:Решение: найдём область определения:

Ответ: 
Пример 8:Решение: решим неравенство  . Парабола
. Парабола  пересекает ось абсцисс в точках
пересекает ось абсцисс в точках  . Поскольку
. Поскольку  , то ветви параболы направлены вниз.
, то ветви параболы направлены вниз.
Ответ: область определения: 
Примечание: Неравенства вида  и
и  (+ такие же строгие неравенства + неравенства с противоположными знаками), где
(+ такие же строгие неравенства + неравенства с противоположными знаками), где  – положительное число, легко решаются аналитически.
– положительное число, легко решаются аналитически.
Перенесём «единицу» в правую часть:  .
.
Умножим обе части неравенства на –1:  .
.
Из каждой части извлекаем квадратный корень, при этом «икс» необходимо заключить под знак модуля:  .
.
Согласно правилу раскрытия модуля, которое можно найти в школьных формулах:
 , то есть в итоге и получен наш отрезок
, то есть в итоге и получен наш отрезок  .
.
Пример 10:Решение: решим неравенство  . Парабола
. Парабола  касается оси
касается оси  в точке
в точке  , причём, ветви параболы направлены вверх. Таким образом, функция
, причём, ветви параболы направлены вверх. Таким образом, функция  не определена в единственной точке.
не определена в единственной точке.
Ответ: область определения 
Пример 12: Решение: составим и решим систему:


Ответ: область определения: 
Пример 14: Решение: составим и решим систему:


Ответ: область определения 
Примечание: неравенство  разрешимо как с помощью анализа расположения параболы
разрешимо как с помощью анализа расположения параболы  относительно оси абсцисс, так и аналитически.
относительно оси абсцисс, так и аналитически.
Перенесём «двойку» в правую часть:  . Из каждой части извлечём квадратный корень, при этом «икс» необходимо заключить под знак модуля:
. Из каждой части извлечём квадратный корень, при этом «икс» необходимо заключить под знак модуля:  . Согласно правилу раскрытия модуля (см. Горячие формулы школьного курса математики):
. Согласно правилу раскрытия модуля (см. Горячие формулы школьного курса математики):  , что в точности соответствует объединению интервалов
, что в точности соответствует объединению интервалов  .
.
Пример 16: Решение: область определения функции задаётся системой:


Ответ: 
Пример 18: Решение: составим и решим двойное неравенство:

Ответ: область определения: 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)