Максимальная дальность действия РЛС в свободном пространстве.

Основным уравнением радиолокации называется уравнение, связывающее максимальную дальность действия активной РЛС в свободном пространстве с ее основными техническими характеристиками и отражающей способностью объекта.

Допустим в точке О расположен передатчик РЛС, излучающий импульсную мощность PI, а в точке О1, расположенной на расстоянии Dот РЛС, находится отражающий объект (рис.4.1).

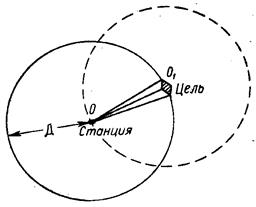
Рис.4.1. Определение максимальной дальности действия РЛС.

 

В случае ненаправленной передающей антенны РЛС плотность потока мощности П0 на расстоянии D от станции:

П0 = ,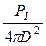

где: 4πD2 – площадь поверхности сферы.

Для направленной антенны плотность потока мощности П1 в направлении максимального излучения:

П1 = ,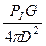

где: G –коэффициент направленного действия (КНД) антенны.

КНД антенны G представляет собой выигрыш в плотности потока мощности, который дает антенна направленного действия по сравнению с ненаправленной антенной.

При облучении объект (цель) становится вторичным излучателем, и часть рассеянной им энергии принимается приемником РЛС в виде отраженного сигнала. В связи со сложностью реальных радиолокационных целей направленностью вторичного излучения обычно пренебрегают.

Свойства цели как вторичного излучателя характеризуются ЭПР цели σ. Тогда мощность отраженного сигнала:

P0 = П1σ

Соответственно плотность потока мощности, создаваемая отраженным сигналом в приемной антенне:

П2 = =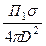

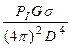
Отсюда мощность отраженного от цели сигнала, принятого антенной:

PS = П2 SA,

где: SA – эффективная площадь антенны.

Эффективная площадь антенны SA – это площадь идеальной синфазной поверхности в плоскости раскрыва антенны. Так как эффективная площадь антенны прямо пропорциональна геометрической площади антенны, то чем выше направленность антенны, тем больше ее эффективная площадь.

Отсюда:

PS =

При решении этого уравнения относительно дальности до цели:

D =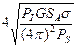

Допустим, чтоPmin – это минимальное значение мощности отраженного сигнала в антенне, при которой он может быть обнаружен на фоне внутренних шумов приемника РЛС. Тогда расстояние до цели, при котором PS = Pmin, является максимальной дальностью действия РЛС.

Таким образом, максимальная дальность действия РЛС:

Dmax =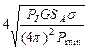

Данное выражение называется основным уравнением радиолокации.

Основное уравнение радиолокации показывает, что максимальная дальность действия РЛС в свободном пространстве зависит от параметров РЛС и отражающих свойств цели. Максимальная дальность действия РЛС тем выше, чем больше излучаемая мощность передатчика, КНД антенны, ЭПР цели и чем меньше значение чувствительности приемника.

Однако все указанные величины находятся под корнем четвертой степени. Поэтому добиться существенного увеличения максимальной дальности действия РЛС за счет изменения этих параметров весьма трудно. Так, например, для увеличения дальности действия РЛС в 2 раза необходимо увеличить мощность передатчика или улучшить чувствительность приемника в 16 раз.

Данное обстоятельство имеет и свои положительные стороны. В частности, на дальность действия РЛС мало влияют возможные отклонения стоящих под корнем величин. Так, например, при уменьшении мощности передатчика в 2 раза дальность действия РЛС снижается только в 1,2 раза. По той же причине разница в дальности действия по целям, которые существенно отличаются по ЭПР, сравнительно невелика.

Рассмотрим влияние технических характеристик РЛС на ее максимальную дальность действия более подробно.

Из основного уравнения радиолокации следует:

Dmax ~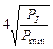

Импульсная мощность PI связана со средней мощностью передатчика выражением:

,

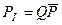где: Q = = 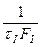– скважность импульсов.

Тогда:

Dmax ~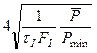

При анализе этого выражения можно сделать ошибочный вывод о том, что большую дальность действия РЛС можно получить за счет уменьшения длительности импульса передатчика τI. Однако фактически с длительностью зондирующего импульса связана не только импульсная мощность передатчика, но и чувствительность приемника РЛС.

Действительно, длительность импульса обратно пропорциональна эффективной ширине его спектра. Поэтому при уменьшении длительности импульса расширяется его частотный спектр. Следовательно, для приема отраженного от цели сигнала должна быть увеличена полоса пропускания приемника РЛС, но это приводит к пропорциональному возрастанию мощности шумов на входе приемника и ухудшению его чувствительности, т.е.:

Pmin ~ 1/τI

Отсюда:

Dmax ~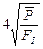

Следовательно, длительность зондирующего импульса τI на максимальную дальность действия РЛС не влияет.

С другой стороны, из выражения для средней мощности передатчика следует:

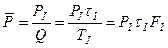
Отсюда:

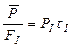
Но произведение импульсной мощности PIна длительность импульсаτIпредставляет собой полную энергию импульса.

Следовательно, дальность действия РЛС определяется не мощностью зондирующего импульса, а его энергией. В частности, при одинаковой средней мощности излучения РЛС с импульсным режимом работы не дает выигрыша в дальности действия по сравнению с РЛС непрерывного излучения.

Рассмотрим выражение:

Dmax ~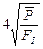

Отсюда следует, что при заданной средней мощности передатчика увеличение дальности действия РЛС возможно также за счет уменьшения частоты следования зондирующих импульсов FI. Это связано с тем, что при этом увеличивается время накопления энергии в модуляторе генератора и соответственно увеличивается излучаемая в импульсе энергия.

Однако частота следования зондирующих импульсов FIопределяет вероятность обнаружения цели. В частности, чем выше частота следования, тем лучше условия обнаружения цели. Поэтому возможности выигрыша в дальности действия РЛС за счет уменьшения частоты следования импульсов весьма ограничены.

Выводы:

1. Увеличение максимальной дальности действия РЛС возможно только за счет увеличения энергии зондирующих импульсов путем увеличения средней мощности передатчика (т.е. за счет увеличения мощности источника питания).

Преобразуем основное уравнение радиолокации. КНД параболической антенны и эффективная площадь антенны связаны выражением:

G =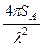

Отсюда:

Dmax =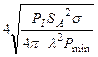

Следовательно,

Dmax~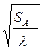

Таким образом: