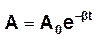Теоретичні відомості

Звіт

про виконання лабораторної роботи

по темі: «Затухаючі коливання»

 

Виконала:

ст. гр. ПФ-21

Наконечна О.М.

Перевірив:

Когут З.О.

 

 

Львів 2013

Мета:ознайомитись з теорією затухаючих коливань, змінюючи вхідні параметри побудувати графіки та проаналізувати їх поведінку.

Обладнання: Програма MATLAB.

Теоретичні відомості

Реальні механічні коливання здійснюються при наявності сил опору середовища. Тому механічна енерґія коливної системи з часом зменшується, а самі коливання загасають. Сила опору середовища переважно пропорційна швидкості руху тіла, що здійснює коливання:

, (3.32)

де r – коефіцієнт опору середовища,

знак ( - ) вказує на протилежний напрям сили опору

і швидкості руху.

Нехай тіло масою m під дією пружної сили -kxі сили опору 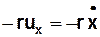здійснює коливання вздовж осі OX. Рівняння руху такого тіла:

, (3.33)

або: . (3.34)

Позначивши:

; ,

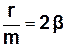де - коефіцієнт згасання,

запишемо диференціальне рівняння згасаючих коливань:

. (3.35)

Якщо 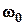> ,розв’язком (3.35) є рівняння:

 

φ₀), (3.36)

яке описує гармонічні коливання з циклічною частотою 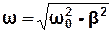і змінною у часі амплітудою 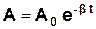при початко-

вій амплітуді А₀ (рис.3.4)

T

An+1

An

A0

t

Рис.1

 

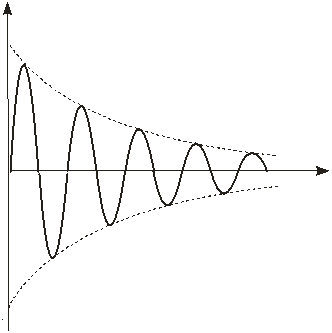
Період згасаючих коливань: 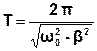. (3.37)

· Декрементом згасання D називається відношення амплітуд двох послідовних коливань:

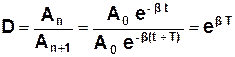. (3.38)

· Лоґарифмічним декрементом згасання називається фізична величина:

. (3.39)

· Часом релаксації коливальної системи 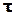називається проміжок часу протягом якого амплітуда коливань зменшується в е разів (е– основа натурального лоґарифму)

 

· Коефіцієнтом згасання називається фізична величина, обернена до часу релаксації:

. (3.40)

· N_е – число коливань, після здійснення яких амплітуда зменшується в е разів, так що 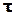=N_еT.

= Т= .(3.41)

Отже лоґарифмічний декремент згасання - це фізична величина, обернена до числа коливань N_e, після здійснення яких амплітуда зменшується в е разів.

· Добротністю системи називається фізична величина:

,(3.42)

де Е – енерґія системи у даний момент часу;

E – енерґія, втрачена протягом одного періоду.

Отже добротність системи тим більша, чим менші втрати

енерґії системи E.Можна показати, що:

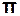= N_e . (3.43)

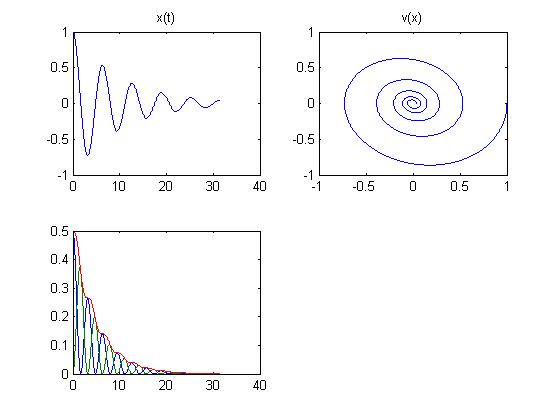
1. >>

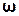Код програми складається з трьох файлів:

1. function a=OdnomirOsc(t,x) %Рівняння руху

% опис функції

global W0 beta

a=zeros(2,1);

a(1)=x(2); %Швидкість

a(2)=-W0^2*x(1)-2*beta*x(2); %Прискорення

 

2. function E=EnergyOd(W0,L,M)

K=length(M); % число стрічок матриці розв'язків

K1=1; % час

for j=1:3 % ланка

for i=1:K % час

if j==1

e(i)=0.5*L*(M(i,1).^2); %потенціальна енергія

end;

if j==2

e(i)=0.5*(L/(W0^2))*(M(i,2).^2); %кінетична енергія

end;

if j==3

e(i)=0.5*(L/(W0^2))*(M(i,2).^2)+0.5*L*(M(i,1).^2); %повна енергія

end;

end;

en(:,K1)=e'; %транспонуємо е

K1=K1+1;

end;

E=en;

 

3. global W0 L beta

W0=1; % Задання частоти коливної системи

L=1; % Жорсткість пружини і т.д.

beta=0.1;

q0(1)=1; %Початкові

q0(2)=0; %умови

Tfin=10*pi; %права границя часової сітки

Np=2^13-1; % число вузлів часової сітки

[T,M]=ode45('OdnomirOsc',[0:Tfin/Np:Tfin],q0);

E=EnergyOd(W0,L,M);

%Розрахунок похибки чисельного методу

for i=1:Np+1

s=E(i,3); %Повна енергія у момент часу і

E0=0.5*(L/(W0^2))*(q0(2)^2)+0.5*L*(q0(1)^2);

%Початкова повна енергія системи

E1(i)=((E0-s)/E0)*100; %Відносна похибка методу у відсотках

end;

max(E1) %Максимальна відносна похибка методу у відсотках

%Побудова графіків

subplot(2,2,1); plot(T,M(:,1)); title('x(t)');

%Залежність координати від часу

subplot(2,2,2); plot(M(:,1),M(:,2));title('v(x)'); %Фазовий портрет

subplot(2,2,3); plot(T,E(:,1),T,E(:,2),T,E(:,3)); %Повна, кінетична, потенціальна ене-ргії

 

Отриманий результат:

Отже, ми отримали згасаючі коливання. Оскільки: коливання відбуваються зі зменшенням амплітуди, фазовий портрет є стійким фокусом, а потенціальна та кінетична енергії змінюються за періодичним законом зі зменшенням повної енергії.

 

2. ≈

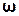Код програми складається з трьох файлів:

1. function a=OdnomirOsc(t,x) %Рівняння руху

% опис функції

global W0 beta

a=zeros(2,1);

a(1)=x(2); %Швидкість

a(2)=-W0^2*x(1)-2*beta*x(2); %Прискорення

 

2.function E=EnergyOd(W0,L,M)

K=length(M); % число стрічок матриці розв'язків

K1=1; % час

for j=1:3 % ланка

for i=1:K % час

if j==1

e(i)=0.5*L*(M(i,1).^2); %потенціальна енергія

end;

if j==2

e(i)=0.5*(L/(W0^2))*(M(i,2).^2); %кінетична енергія

end;

if j==3

e(i)=0.5*(L/(W0^2))*(M(i,2).^2)+0.5*L*(M(i,1).^2); %повна енергія

end;

end;

en(:,K1)=e'; %транспонуємо е

K1=K1+1;

end;

E=en;

 

3.global W0 L beta

W0=1; % Задання частоти коливної системи

L=1; % Жорсткість пружини і т.д.

beta=0.99;

q0(1)=1; %Початкові

q0(2)=0; %умови

Tfin=10*pi; %права границя часової сітки

Np=2^13-1; % число вузлів часової сітки

[T,M]=ode45('OdnomirOsc',[0:Tfin/Np:Tfin],q0);

E=EnergyOd(W0,L,M);

%Розрахунок похибки чисельного методу

for i=1:Np+1

s=E(i,3); %Повна енергія у момент часу і

E0=0.5*(L/(W0^2))*(q0(2)^2)+0.5*L*(q0(1)^2);

%Початкова повна енергія системи

E1(i)=((E0-s)/E0)*100; %Відносна похибка методу у відсотках

end;

max(E1) %Максимальна відносна похибка методу у відсотках

%Побудова графіків

subplot(2,2,1); plot(T,M(:,1)); title('x(t)');

%Залежність координати від часу

subplot(2,2,2); plot(M(:,1),M(:,2));title('v(x)'); %Фазовий портрет

subplot(2,2,3); plot(T,E(:,1),T,E(:,2),T,E(:,3)); %Повна, кінетична, потенціальна ене-ргії

 

Отриманий результат:

При критичному режимі коливань спостерігаємо найшвидше повернення системи в положення рівноваги.

3. <

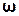Код програми складається з трьох файлів:

1. function a=OdnomirOsc(t,x) %Рівняння руху

% опис функції

global W0 beta

a=zeros(2,1);

a(1)=x(2); %Швидкість

a(2)=-W0^2*x(1)-2*beta*x(2); %Прискорення

 

2.function E=EnergyOd(W0,L,M)

K=length(M); % число стрічок матриці розв'язків

K1=1; % час

for j=1:3 % ланка

for i=1:K % час

if j==1

e(i)=0.5*L*(M(i,1).^2); %потенціальна енергія

end;

if j==2

e(i)=0.5*(L/(W0^2))*(M(i,2).^2); %кінетична енергія

end;

if j==3

e(i)=0.5*(L/(W0^2))*(M(i,2).^2)+0.5*L*(M(i,1).^2); %повна енергія

end;

end;

en(:,K1)=e'; %транспонуємо е

K1=K1+1;

end;

E=en;

 

3.global W0 L beta

W0=0.01; % Задання частоти коливної системи

L=1; % Жорсткість пружини і т.д.

beta=1;

q0(1)=1; %Початкові

q0(2)=0; %умови

Tfin=10*pi; %права границя часової сітки

Np=2^13-1; % число вузлів часової сітки

[T,M]=ode45('OdnomirOsc',[0:Tfin/Np:Tfin],q0);

E=EnergyOd(W0,L,M);

%Розрахунок похибки чисельного методу

for i=1:Np+1

s=E(i,3); %Повна енергія у момент часу і

E0=0.5*(L/(W0^2))*(q0(2)^2)+0.5*L*(q0(1)^2);

%Початкова повна енергія системи

E1(i)=((E0-s)/E0)*100; %Відносна похибка методу у відсотках

end;

max(E1) %Максимальна відносна похибка методу у відсотках

%Побудова графіків

subplot(2,2,1); plot(T,M(:,1)); title('x(t)');

%Залежність координати від часу

subplot(2,2,2); plot(M(:,1),M(:,2));title('v(x)'); %Фазовий портрет

subplot(2,2,3); plot(T,E(:,1),T,E(:,2),T,E(:,3)); %Повна, кінетична, потенціальна ене-ргії

 

Отриманий результат:

Графіки демонструють аперіодичний процес, характерний для руху у середовищі з великою дисипацією.