Вихідні дані

ЛАБОРАТОРНА РОБОТА № 6

Апроксимація емпіричного розподілу теоретичним законом.

Розрахунок інтервальних теоретичних частот III типу розподілів Пірсона

Вихідні дані

і
x_i	-11.6	-9.3	-6.9	-4.6	-2.3	0.0	2.3	4.6	6.9	9.3
m_i

На основі емпіричного розподілу середньодобових температур повітря за 4 березня розрахувати інтервальні теоретичні частоти (m_i) та інтервальні ймовірності (p_i) III типу розподілів Пірсона, тобто побудувати теоретичний розподіл у координатах (x_i ; m_i , i =1,k).

Щоб удосконалитися у виборі теоретичного розподілу, треба проаналізувати статистичні оцінки моментів розподілу, а також побудувати полігон розподілу випадкової величини, що досліджується.

На основі графічного представлення емпіричного (x_i ; m_i , i =1,k) й теоретичного (x_i ; m_i , i =1,k) розподілів (полігонів) зробити висновок про якісні розбіжності між емпіричними m_i й теоретичними m_i частотамиIII типу розподілів Пірсона.

Важливе значення при дослідженнях властивостей випадкової величини має об’єм сукупності, до якої добирається теоретичний закон. Цей ряд обов’язково повинен бути дійсно вибіркою з генеральної сукупності і мати такий об’єм, який дозволяв би провести оцінку параметрів із заданою точністю, тобто отримати вірогідні характеристики.

Таким чином, було здійснено перехід від простої статистичної сукупності до згрупованого ряду, який складається з 99 членів (n = 221).

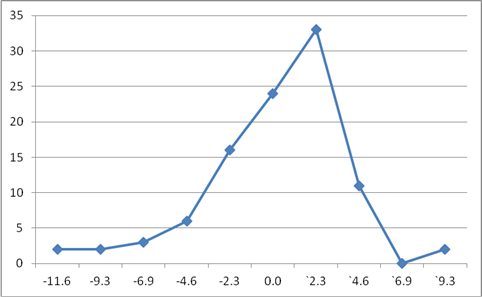
Рис. 1. Полігон розподілу емпіричних частот m_i середньодобових температур повітря за 4 березня.

Із рис. 1 випливає, що розподіл емпіричних частот не є симетричним (As = r₃ = -0,8). Коефіцієнт ексцесу складає: E = r₄ – 3 = 4.3 – 3 = 1.3, тобто крива є витягнутою. Щоб переконатися в правильному виборі типу розподілів Пірсона, необхідно розрахувати статистику S за формулою (3.24) і статистику капа ae за формулою (3.23):

S =	6(4.3 + 0.8²- 1)*	=34.8.
3(-0.8)²- 24.3 + 6

ae =	(-0.8)²(*3.7+ 2)²	=0.28.
16(*3.7+ 1)

Формулюємо гіпотезу про можливість апроксимації емпіричного розподілу III типом розподілів Пірсона.

Для III типу розподілів Пірсона основне рівняння для інтервальних теоретичних частот має вигляд:

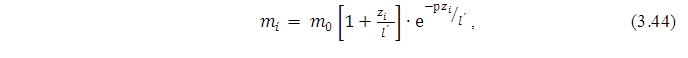де p, l΄, m₀ – параметри цього розподілу;

z_i – змінна, яка розраховується так:

де:

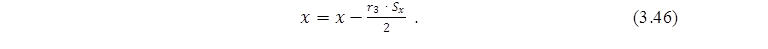Таким чином, статистика x за формулою (3.46) дорівнює:

x = 10.3 -	-0.8 3.7*	=11.78.
2

Параметр форми p визначається рівнянням (3.47):

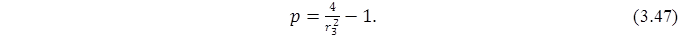Із цього випливає:

p =	4	- 1 =4.0.
0.8

Параметр масштабу l΄ розраховується таким чином:

Величину σ розраховуємо за формулою (3.35). Виходячи зі значень середнього квадратичного відхилу S_x = 3.7та довжини часткового інтервалу c = 2,0, вона дорівнює:

σ = 3.7/ 2.3 = 1.61.

За формулою (3.48) маємо:

l` = 1.61 * (-2.5+0.4) = - 3.38.

У нашому випадку крива розподілу відноситься до другої групи кривих III типу розподілів Пірсона, тобто l΄ ˂ 0 (розподіл має лівосторонню асиметрію). При цьому параметр форми р > 1.

Параметр m₀ – це теоретична частота за умови z_i = 0, яку можна отримати за допомогою рівняння (3.49):

в якому Г(х) – гамма-функція відповідного аргументу. Її значення для заданого x знаходяться в додатку К. Значення гамма-функції розраховується за формулою:

Г(х) = (х – 1) * Г(х – 1).

Г(р + 1) = Г(4 + 1) = Г(5) = 4 * Г(4) = 4 * 3 * Г(3) = 4 * 3 * 2 * Г(2) = 4 * 3 * 2 * 1 = 24.

Отже, за формулою (3.49) теоретична частота m₀ за умови z_i = 0 складатиме:

m₀₌	99	*	4⁵	= 22.8.
3.38	2.72⁴ 24*

За допомогою основного рівняння III типу розподілів Пірсона (3.44) були отримані інтервальні теоретичні частоти m_i (9-й стовпчик) та інтервальні ймовірності p_i (10-й стовпчик). В 11-ому стовпчику цієї таблиці наведені значення функції розподілу отриманого теоретичного закону, тобто III типу розподілів Пірсона, для випадкової величини, що досліджується.

Результати розрахунків інтервальних теоретичних частот та інтервальних імовірностей III типу розподілів Пірсона на основі емпіричного розподілу середньодобових температур повітря за 4 березня.

Статистики ряду та оцінки параметрів

S_x

r³

r⁴

m₀

2.3

-2.0

3.7

-0.8

4.3

1.61

34.8

0.28

4.0

- 3.38

-1.36

22.8

Розрахунки інтервальних теоретичних частот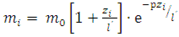

і	х_і	т_і	z_i	1+(z_i/l`)	(1+(z_i/l`))^р	-pz_i/l`	е^-^pzi/l`	m_i	p_i	P(X˂x)

	-11.6		-4.45	2.31	28.47	-5.26	0.005	0.26	0.003	0.003
	-9.3		-3.45	2.02	16.64	-4.08	0.016	0.74	0.007	0.010
	-6.9		-2.40	1.71	8.55	-2.84	0.058	1.86	0.018	0.028
	-4.6		-1.41	1.41	3.95	-1.67	0.18	5.78	0.058	0.086
	-2.3		-0.41	1.12	1.57	-0.48	0.62	15.8	0.16	0.246
	0.0		0.59	-0.83	0.47	0.70	2.0	-37.8	-0.4	-0.154
	2.3		1.59	-0.53	0.08	1.88	6.6	-79.8	-0.8	-0.954
	4.6		2.60	-0.23	0.002	3.08	21.8	-114.3	-1.2	-2.154
	6.9		3.60	0.07	0.00002	4.26	71.0	113.3	1.1	-1.054
	9.3		4.64	0.37	0.02	5.49	243.1	204.9	2.07	1.01

Рис. 10. Полігони розподілу емпіричних m_i (------) і теоретичних m_i (- - - -) частот III типу розподілів Пірсона.

Порівняння емпіричних і теоретичних інтервальних частот свідчить про те, що між ними є значні якісні відмінності. Тому робимо висновок: емпіричний розподіл даної метеорологічної величини неможливо апроксимувати III типом розподілів Пірсона.