ТЕОРИЯСЫ

XII ТАРАУ

ГАЗДАРДЫҢ ЭЛЕМЕНТАР КИНЕТИКАЛЫҚ

ТЕОРИЯСЫ

Молекула-кинетикалық теория заттың ең қарапайым газ түріндегі күйін түсіндіруде зор табыстарға жетті. Кинетикалық теория, тіптен өзінің элементар жеңілдетілген түрінде де газ күйіндегі заттың негізгі қасиеттерін және газда болып өтетін құбылыстарды сапа жағынан ғана емес, сандық жағынан да (бipгe жуық сандық коэффициентке кебейтуге дейін дәлдікпен) түсіндіре алады.

Біздің алға койғалы отырған бірінші мақсатымыз газдың ыдыс қабырғаларына түсіретін қысымын есептеп шығару болып табылады. Бұл мәселені шешу абсолют температураның физикалық, табиғатын тусіруге де көмектеседі

§ 99. Газдардың кинетикалык теориясының қысым

үшін теңдеуі

Газдың ең қарапайым молекула-кинетикалык моделі төмендегідей болады. Газ дегешміз бірдей, хаосты қозғалыстағы, өзара жанасқанша бір-бірімен әрекеттеспейтін молекулалардың жиынтығы. Молекулалардың мелшерлері өте аз, сондықтан да олардың қорытқы көлемін, ыдыстың көлемімен салыстырғанда, ескермеуге болады. Молекулалардың әркайсысы кейде бір-біріне немесе ыдыстың қабырғасына сершмді соктыққаны болмаса, уакытыңың басым көпшілігін еркін қозғалыста өткізеді.

Бұл айтылып отырған моделіміз идеал газдың мо­делі. Нақты газдардың молекулаларының шектік өлшемдері бар және олар бір-бірінен өз ара алыстаған кезде тез әлсірейтін күшпен әрекеттесіп отырады. бірақ тығыздық азайған сайын молекулалардың меншікті көлемі газдың алып тұрған келемінен азая түседі ал мо­лекулалардың орташа кашыктықтарының ұлғаятыны соншалыкты, олардың арасындағы өз ара әрекеттесу күштерш ескермеуге де болады. Демек, кез келген газ идеал газға жакын болатын жағдайда жоғарыда сипатталған моделдің негізіндегі біздің ойларымыз дұрыс бо­лады екен.

Молекула ыдыстың қабырғасына соққан кезде, ол одан сайын күш өз импульсының өзгерісіне тең импульс береді. Қабырға бетінің әрбір ΔS элементіне көп мөлшерде молекулалар үздіксіз соғылады да, осының арқасында ол Δt уакытта ΔS-ке нормаль бойынша бағытталғанда қорытқы ΔК импульс алады. Механикадан білетініміздей, ΔК-ның Δt-ге қатынасы ΔS-ке әсер етстін күшті, ал осы күштің ΔS-ке қатынасы р қысымды береді

Молекулалар ретсіз хаосты қозғалады; қозғалыс бағыттарының ықтималдығы бірдей, олардың кайсысының да баскаларынан ешбip артықшылығы жоқ. Бұлай дейтін себебіміз ыдыстың қабыррасына түсірілген қысым барлық жерлерде де бірдей болады. Егер қайсыбір бағытта молекулалар қозғалысы басым болса, онда ыдыс қабырғасының осы учаскесіне түсірілген қысым да артық болар еді.

Молекулалардың жылдамдықтарының шамалары әр түрлі бола алады. Сонымен қатар, әpбip соқтығыстан кейін молекуланың жылдамдығы өзгеріп отыруы Tйіc, әpi жылдамдыктың өсу немесе азаю мүмкіншіліктері де бірдей болады. Бұл екі молекуланың кинетикалық энергияларының косындысының соктығысқанға дейін де, соқтырысканнан кейін де бірдей болуы тйіс екендігін шығарады. Демек, бip молекуланың жылдамдығы артқан кезде, екінші молекуланың жылдамдығы кемиді

Койылған мәселені шешуін оңайлату үшін біз молекулалардың козғалысына қатысты кейбір жеңілдететін шарттарды еңгіземіз. Біріншіден, молекулаларды өз ара перпендикуляр үш бағытта қозғалады деп есептейміз. Егер газдың N молекуласы болса, онда уакыттың кез

 

келген мезгілінде әрбір бағытпен N/3молекула, ал олардың

бірінші жартысы (яғни,N/6молекула) берілген бағытпен бip жаққа, ал екінші жартысы — екінші жаққа козғалады (219-сурет). осындай ұйғарымды суйене отырып,біз қарастырғалы отырған

_________

■ Массалары бірдей екі шардың cерпімді центрлік соктығысуы кезінде, шарлардың энергия алмасатындығын ескерте кетейік.

 

бағытта (мәселен, ΔS кабырғаның берілген элементіне нормаль бойымен) моле­кулалардың 1/6 бөлігі қозғаладыдеп есептейміз.

Екіншіден, барлық молекулалардың v жылдамдықтарының мәндерін бірдей деп аламыз.

Келесі параграфта керсететініміздей, алғашқы шарткысымды есептеуді ақырғы нәтижесіне әсер етпейді; екінші шартты қарастырмаудың қандай нәтижеге әкепсоғатынын осы параграфта баяндаймыз.

ыдыстың қабырғасына соққан молекуланың оған беретін импульсын есептеп шығарайық. қабырғаға соқтыққанға дейінгі молекуланың импульсы сыртқы нормаль бойымен ΔS-ке қарай бағытталған және mv-ге тең болады. Соқтығыстан кейін молекуланың им­пульс таңбасы өзгереді. Сөйтіп,молекула импульсының өciмшeci мынаған тең болады:

 

, (99.1)

 

Ньютонның үшінші заңы бойынша, кабырға соқтығысу кезінде нормаль бойымен бағытталған 2mv импульс алады.

Δt уақытта қабырраның ΔS элементіне дейін осы бағытта козғалып келе жатқан ( табаны ΔS, биіктігі vΔt цилиндрдің ішіндегі) барлық молекулалар келіп жетеді (221-сурет). бұл молекулалардың саны мынаған тең болады:

(99.2)

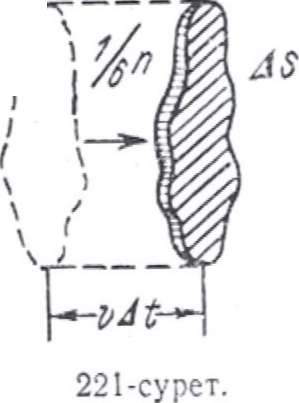Мұндағы n — бірлік келемдегі молекулалар саны. шынында молекулалардыңбip бөлігі кабырғаға жетем дегенше баска молекулалармен соқтығысып,өзінің бағытын өзгертеді де ΔS-ке жете алмайды деген қарсы пiкiрайтуға да болады. алайда соқтығысулар молекулалар­дың хаосты қозғалысының сипатын езгерте алмайды:кабырғаға қарай беттеген молекулалар тобының кейбіреулерінің басқа барығыттарда козғалатын молекулалар тобына өтуі,дәл сол шамалы молекулалардың басқа топтарынан, кабырғаға қарай беттеген молекулалар тобына өтуімен катар журеді. Сондыктан кабырғаға келіп жететін молекулалардың санын есептеген кезде молекулалардың бір-бірімен соқтығысуларын ескермеуге болады. (99.2) бойынша бірлік уақыттың ішінде ΔS ауданға келіп соғатын молекулалар саны мынаған тең болады:

 

 

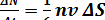
ал бip секунд ішінде бірлік ауданға(ΔS= 1 м²) келіп соқтығатын молекула­лар саны

 

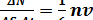(99.3)

 

(99.2)-дегі соқтығысулар санын әрбір соктығысудан кабырғаға берілетін (99.1)-дегі импульсқа көбейтіп, Δt уақытта кабырғаның ΔS элементіне берілетін қосынды ΔК импульсты анықтаймыз.

ΔK импульстың Δt уакытқа қатынасын алып, ΔS-ке әсер етуші күшті табамыз. ақыры, табылған күштің ΔS ауданға қатынасын алып, ыдыстың қабырғасына түсірілген газдың қысымын табамыз. демек,

(99.4)

=nv=mv²/2 шамасының молекуланың ілгерілмелі қоз­ғалысының кинетикалық энергиясы екенін ескере отырып, кысымның өрнегін темендегідей түргекелтіруге бо­лады:

(99.5)