Пример 2

Исследование функций с помощью производной

 

Условия постоянства функции на промежутке

Теорема. Пусть функция f(x) определена и непрерывна на некотором промежутке X , 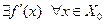X₀ – множество внутренних точек.

Тогда:

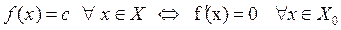
Доказательство:

Необходимость

По условию f(x)=с , ( 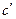) = 0

 

Достаточность

Пусть 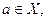a – произвольная точка. f(a)=с – число. Возьмём 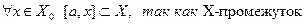на [a,x] выполняются условия теоремы Лагранжа:

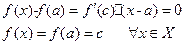так как f `(c)=0

 

Пример 1

y=arcsin(x) + arсcos(x) – определена на промежутке [-1; 1], непрерывна и дифференцируема как сумма двух непрерывных функций

 

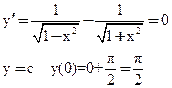
Пример 2

Область определения x ≠ ±1

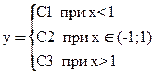
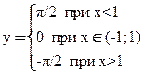
Теорема 1.Критерий монотонности.

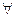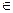Пусть функция f(x) определена и непрерывна на промежутке X, дифференцируемa в x X₀

Тогда:

f(x) - неубывающая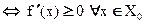

 

Доказательство

Необходимость

 

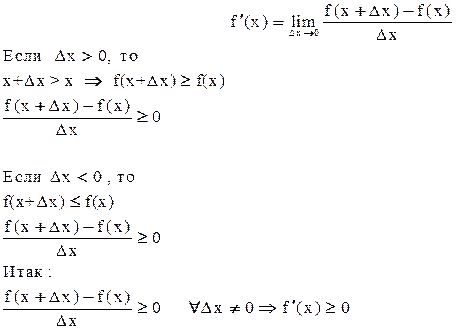
Достаточность

Возьмём x₁ X₀ и x₂ 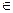X₀ такие, что x₁<x₂ 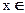[x₁, x₂] удовлетворяют условиям теоремы Лагранжа:

f(x₂)-f(x₁)=f `(c)( x₂ - x₁) ≥ 0 ,

так как f `(c) ≥0 и ( x₂ - x₁) ≥0 . По теореме Лагранжа x₁ < с < x₂ , следовательно

f(x₂) ≥ f(x₁)

значит, функция неубывающая по определению.

 

 

Теорема 2. Критерий строгой монотонности

Пусть функция f определена и непрерывна на промежутке X, дифференцируема в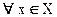

Тогда:

f(x) возрастет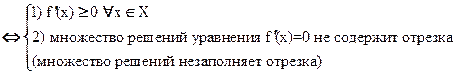

Доказательство

Необходимость

f возрастает при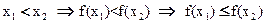

по теореме 1 (предыдущая)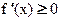

Покажем, что множество решений 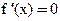не содержит отрезка. Допустим, что 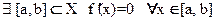, из условия постоянства функции на промежутке 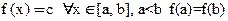- противоречит строгому возрастанию.

Достаточность

Так как 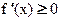, то по предыдущей теореме(Критерий монотонности)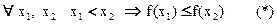

Допустим, что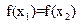

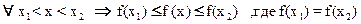
f(x)=c, на [x₁ ,x₂] – противоречит не условию, следовательно в (*) не может быть равенства, следовательно 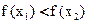, значит функция строго возрастает