Законы распределения времени выполнения работ сетевого графика ТЭП

Наименование распределения	Приближенные формулы расчета Параметров
Логарифмически-нормальное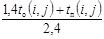
Усеченное нормальное
Треугольное

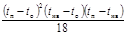
Рассмотренные выше зависимости позволяют по оценкам продолжительности работ сетевого графика, задаваемым соответствующими исполнителями (специалистами), определить математическое ожидание времени выполнения 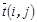и дисперсию 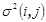этих работ, значения которых являются исходными данными для расчета параметров вероятностных сетевых моделей.

Таким образом, зная и , можно рассчитать временные параметры сетевых графиков ТЭП и оценить вероятность их реализации с заданными характеристиками.

Так, при достаточно большом количестве работ, принадлежащих пути L, и выполнении некоторых общих условий можно применить центральную предельную теорему Ляпунова, согласно которой закон распределения суммы независимых случайных величин с увеличением числа слагаемых приближается к нормальному закону при условии, что каждое слагаемое в одинаковой степени мало по сравнению с суммой. Сетевые графики ТЭП в большинстве случаев отвечают таким допущения, так как критический путь состоит из достаточно большого числа работ, продолжительности которых представляют собой равномерно малые независимые случайные величины, а, следовательно, предположение о нормальном законе распределения момента его окончания (наступления завершающего события сетевого графика ТЭП) можно считать правомерным.

На основании этого можно утверждать, что среднее значение продолжительности пути будет равно сумме средних значений продолжительности работ 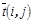, принадлежащих этому пути, с дисперсией 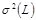, равной сумме соответствующих дисперсий :

; (2.30)

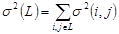. (2.31)

Однако необходимо помнить, что в каждом конкретном технологическом процессе возможны заметные отклонения длины критического пути от ее среднего значения, причем, чем больше суммарная дисперсия продолжительности работ критического пути, тем более вероятны значительные отклонения по абсолютной величине. Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров сети.

Весьма важной задачей анализа вероятностных сетевых моделей становится оценка того, что срок выполнения ТЭП t_кр не превзойдет заданного директивного срока Т_д или определения вероятности наступления завершающего события к требуемому директивному сроку.

Предполагая, что t_кр является случайной величиной с нормальным законом распределения, то вероятность попадания нормально распределенной случайной величины X в интервал может быть определена по следующей формуле:

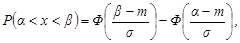(2.32)

где 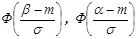- значение стандартной нормальной функции распределения для соответствующих аргументов, или интеграл вероятности

(2.33)

где m и - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины X.

Для вычисления вероятности того, что технологический эксплуатационный процесс будет закончен к заданному сроку Т_д, необходимо определить нижний и верхний пределы диапазона 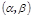возможных значений случайной величины. При этом для определения данного диапазона воспользуемся известным в математической статистике «правилом трех сигма», в соответствии с которым можно принять

(2.34)

где - среднее значение раннего срока наступления завершающего события ТЭП или средняя продолжительность критического пути, которая вычисляется по формуле (2.30);

- среднее квадратическое отклонение продолжительности (длины) критического пути, которое вычисляется по формуле а по формуле (2.31).

Если принять, что, то вероятность завершения технологического эксплуатационного процесса к этому сроку практически равна нулю. Если же 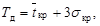то вероятность завершения ТЭП к этому сроку приближается к единице. Следовательно, директивно заданное время не должно выходить за пределы указанного диапазона, т.е.

. (2.35)

Приняв, что , а , и подставив их в формулу (2.32), получим следующее выражение:

(2.36)

Так как второе слагаемое в данном выражении принимает значение, равное Ф(-3) = 0,0014, то этим слагаемым в процессе вычислений можно пренебречь.

Исходя из этого аналитическое выражение для определения вероятности завершения ТЭП к заданному сроку примет следующий вид:

. (2.37)

Геометрически нахождение есть не что иное, как вычисление площади под кривой распределения ограниченной справа Т_д (рис. 14).

 

 

Если принимает значение меньше 0,3, то опасность срыва заданного срока выполнения ТЭП велика, а, следовательно, необходимо принятие дополнительных мер по перераспределению ресурсов, пересмотра состава работ, событий и т.п. Если же значительна (например, более 0,8), то, очевидно, с достаточной степенью надежности можно прогнозировать выполнение ТЭП в установленный срок.

В некоторых случаях представляет интерес и решение обратной задачи: определение планового срока выполнения всего комплекса работ Т_пл с заданной надежностью (вероятностью) .

Для нахождения плановых сроков реализации ТЭП в зависимости (2.37) вместо Т_д подставив Т_пл, получим выражение

или (2.38)

В общем случае можно записать

(2.39)

где - нормированное отклонение случайное величины, определяемое с помощью функции Лапласа ,

(2.40)

Описанным методом можно рассчитывать вероятность наступления к заданному сроку не только завершающего события, но и любого промежуточного (этапного) события сетевого графика ТЭП при сохранении условия, что время выполнения этого этапа, являясь случайной величиной, имеет нормальное распределение.

Однако приведенный метод расчета имеет принципиальные недостатки при оценке параметров даже сложных сетей с большим количеством работ. Дело в том, что на практике нередки случаи, когда дисперсии длины полных путей, близких к критическому, существенно больше, чем . Поэтому при изменении ряда условий возможен переход к новым критическим путям, которые в расчетах не учитывались. Установлено, что если в вероятностном сетевом графике ТЭП имеются подкритические пути, то погрешности расчета по формулам (2.37) и (2.38) могут достигать 15 – 20%.

Следовательно, при анализе сетевых графиков надо учитывать возможность (вероятность) перехода некритических работ (особенно работ с малыми резервами времени) в критические. Такой переход возможен при реализации ТЭП по ряду причин (например: изменение условий выполнения работ; появление отказов; возникновение предпосылок к происшествиям и т.п.).

Ранее было установлено, что признаком принадлежности работы или события к критическому пути является равенство нулю соответствующего резерва времени, т.е.

(2.41)

Расчет величины этой вероятности можно произвести на основании общей формулы (2.32). При этом, учитывая выражение (2.6), примем

Так как значением по-прежнему можно пренебречь, то можно записать:

(2.42)

Зависимость (2.42) определяет вероятность того, что ранний срок наступления события меньше позднего срока наступления этого же события.

return false">ссылка скрыта

Однако в нашем случае требуется определить вероятность отсутствия резерва у события (i), т.е. того, что . Учитывая, что вероятность отсутствия резерва времени [ ] является противоположным событием неравенству , то можно записать:

(2.43)

При этом если при расчетах получено значение вероятности отсутствия резерва времени для события (i), близкое к 0,5, то это значит, что данное событие является потенциально критическим, и, следовательно, таким событиям и работам должно уделяться особое внимание при реализации ТЭП. События, для которых значение близко к нулю, и соответствующие им работы могут быть отнесены в группу наименее напряженных.

Другим эффективным методом анализа вероятностных сетевых моделей является метод статистического моделирования, который основан на последовательных многократных изменениях продолжительности работ (в заданных пределах) и «проигрывании» с помощью электронно-вычислительных средств различных вариантов реализации ТЭП с расчетами всех его временных параметров и коэффициентов напряженности работ. При этом способе продолжительности операций не оцениваются, а выбираются случайным образом по методу Монте-Карло. Эти значения определяются на основании заданных распределений вероятности. Продолжительность эксплуатационного процесса и критический путь рассчитываются для каждой реализованной совокупности операций. Моделирование осуществляется многократно, и каждый раз фиксируется, какие операции являются критическими.

В результате становится возможным определить ожидаемое время выполнения всего комплекса работ ТЭП и его среднеквадратическое отклонение. Кроме того, вместо единственного значения резерва времени для каждой операции определяется интервал этих значений. В то же время, с помощью этой процедуры можно выявить и операции, близкие к критическим, а значит и те операции, задержка в выполнении которых превращает подкритический путь в критический. Процесс «проигрывания» продолжается до тех пор, пока не будет получен приемлемый вариант плана или пока не будет установлено, что все имеющиеся возможности по его улучшению исчерпаны, а достижение поставленных целей ТЭП при заданных условиях реализации - невозможно.

После всестороннего анализа и оптимизации сетевых моделей приступают к разработке календарных план-графиков ТЭП, в соответствии с определенными правилами, которые и рассмотрим в следующем параграфе.

 

5 Разработка календарных план-графиков ТЭП

 

Этап непосредственной разработки календарных план-графиков ТЭП является важным и сложным, так как от качества разработки сетевого графика зависит не только степень соответствия результатов, полученных при расчете параметров сетевой модели, параметрам рассматриваемого технологического процесса, но и достоверность результатов прогнозирования, оперативность и эффективность управления в целом.

В общем случае алгоритм разработки календарных план-графиков технологических эксплуатационных процессов предполагает решение целого комплекса таких задач как:

установление объема работ ТЭП (перечня операций, этапов и других элементов процесса);

выявление взаимосвязей между операциями;

определение последовательности выполнения операций и множества мероприятий безопасности исходя из их взаимосвязи и учета требований к данному процессу;

определение средств, необходимых для реализации процесса;

установление режима работы оборудования, состава инструментов, приспособлений и материалов, используемых при выполнении операций (работ);

оформление разработанной технологии в виде документа, удобного для практического использования и содержащего всю необходимую техническую информацию о процессе.

При этом все задачи сетевого планирования и управления можно условно разделить на задачи анализа и синтеза.

Решение задачи анализа состоит в построении сетевого плана-графика комплекса работ, определении критического пути и выявлении «узких» мест в процессе его реализации, а также возможности (ресурсы) его улучшения.

Решение задачи синтеза предусматривает составление оптимального (в некотором смысле) сетевого плана-графика исходя из заданного критерия качества при условии выполнения заданных ограничений.

Основой для решения задач обоих типов является сетевая модель в виде сетевого графика.

Первый этап разработки сетевого графика начинается с формулирования задания, определяющего конечную цель технологического процесса, на достижение которой должны быть направлены все силы и средства.

В сложных технологических процессах, помимо основной конечной цели, следует четко выделять и промежуточные цели, направленные на решение отдельных частных задач, являющихся составными частями общего процесса. При этом промежуточные цели должны быть взаимосвязаны как по последовательности их достижения, так и по результатам. Когда промежуточных целей несколько, и они в свою очередь могут иметь свои подцели, целесообразно до составления сетевого графика разрабатывать структурную схему всего технологического эксплуатационного процесса. Такая схема позволяет наглядно показать объем и уровни предстоящих работ по их законченным элементам.

Следует заметить, что при составлении сетевых графиков необходимо учитывать не только все взаимосвязи операций, но и требования безопасности, а также имеющиеся в наличии ресурсы.

Начальная информация о планируемом процессе, необходимая для составления сетевого графика, должна содержать объем работ, который выражается перечнем операций (работ) и их взаимосвязью, т.е. последовательностью их выполнения, определяемой установленной технологией реализации ТЭП, а также временные и ресурсные характеристики всего комплекса работ. Такая информация о технологических процессах содержится в эксплуатационной документации, которая разрабатывается предприятиями - разработчиками образцов ВВТ (инструкция, технологические карты и графики, программы и т.д.).

При построении сетевых графиков необходимо соблюдать некоторые правила их построения, а также придерживаться методических рекомендаций, позволяющих оптимизировать процесс разработки календарных план-графиков ТЭП.

Во-первых, сетевые графики рекомендуется строить слева направо, т.е. от исходного события к завершающему, при этом стрелки могут иметь произвольную длину и наклон. Желательно, чтобы конец стрелки находился правее ее начала. Пересечение стрелок допускается, но по возможности этого следует избегать.

Во-вторых, при структурном анализе ТЭП необходимо определить:

1) работы, которые должны быть выполнены до начала данной работы;

2) работы, которые должны быть начаты после выполнения данной работы;

3) работы, которые могут выполняться параллельно, т.е. одновременно с данной работой.

В-третьих, при составлении чернового варианта сетевого графика основное внимание должно уделяться соблюдению логических связей работ. Работы изображаются с таким расчетом, чтобы последующие события располагались правее относительно предшествующих и при этом следует стремиться к возможно меньшему пересечению работ.

После построения чернового варианта сетевого графика необходимо провести упорядочение сетевого графика, которое заключается в таком расположении событий и работ, при котором для любой работы предшествующее ей событие расположено левее и имеет меньший номер по сравнению с завершающим эту работу событием.

Для нумерации событий чаще всего используется метод «вычеркивания» дуг, суть которого рассмотрим на примере некоторого технологического эксплуатационного процесса, включающего 12 событий: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 24 связываю­щие их работы - (0, 1), (0, 2), (0, 3), (1, 2), (1, 4), (1,5), (2, 3), (2, 5), (2, 7), (3, 6), (3, 7), (3, 10), (4, 8), (5, 8), (5, 7), (6, 10), (7, 6), (7, 8), (7, 9), (7, 10), (8, 9), (9, 11), (10, 9), (10, 11).

Как следует из перечня работ, исходным событием сетевого графика является событие 0 (ему не предшествуют никакие рабо­ты), а завершающим - событие 11 (за ним не следует ни одна работа). Полагая на сетевых графиках изменение времени слева направо, поместим событие 0 в левую часть графика, а событие 11 - в правую часть, разместив между ними промежуточные со­бытия в некотором порядке, соответствующемих номерам (рис. 15). События свяжем работами-стрелками в соответствии с перечнем работ.

 

 

 

 

Представленный сетевой график (см. рис. 15) удовлетворяет сформулированным выше правилам, соблюдение которых обязательно при его построении. Однако этот график не полностью упорядочен, так как в упорядоченном сетевом графике все работы-стрелки должны быть направлены слева направо: от событий с меньшими номерами к событиям с большими номерами.

Разобьем условно события сетевого графика на ранги, которые выделим пунктирными линиями и обозначим римскими цифрами (см. рис. 16). Для этого, поместив начальное событие 0в I ранге, мысленно вычеркнем из графика это событие и все, выходящие из него работы-стрелки. Тогда без входящих стрелок останется событие 1, образующее II ранг. Вычеркнув мысленно событие 1 и все выходящиеиз него работы, увидим, что без входящих стрелок остаются события 4 и 2, которые образуют III ранг. Продолжая указанную процедуру вычеркивания, получим IV ранг с событиями 5 и 3, V ранг - с событием 7, VI ранг - с событиями 8 и 6, VII ранг - с событием 10, VIII ранг - с событием 9 и, наконец, IX ранг - с событием 11. При этом видно, что первоначальная нумерация событий не со­всем правильная: так, событие 6 принадлежит к VI рангу и имеет номер, меньший, чем событие 7 из предыдущего ранга. То же можно ска­зать о событиях 9 и 10.

Изменим нумерацию событий в соответствии с их расположе­нием на графике (рис. 16) и получим упорядоченный сете­вой график (рис. 17), в котором над стрелками указывается продол­жительность соответствующих работ (например, в сутках).

 

 

 

 

Порядок нумерации событий, принадлежащих одному рангу, принципиального значения не имеет, поэтому нумерация одного и того же сетевого графика может быть неоднозначной.

После построения сетевой модели и упорядочения номеров событий приступают к расчету параметров сетевого графика в соответствии с формулами, приведенными в п. 3.

 

 

 

 

В большинстве случаев при расчете сетевых моделей ТЭП ограничиваются определением лишь только временных параметров, характеризующих событие, работу и путь. Расчет этих параметров производится в основном вручную, так как все вычисления связаны с выполнением лишь простейших математических операций.

Расчет параметров сетевого графика может быть проведен аналитическим методом, методом расчета непосредственно на сетевом графике, в таблицах и матрицах различной формы, с помощью отдельных карточек и т.д.

Аналитический расчет параметров сетевого графика производится по формулам, представленным в параграфе 3, в следующей последовательности: сначала вычисляются ранние сроки начала и окончания всех событий, начиная от исходного события и кончая завершающим. Затем определяются поздние сроки начала и окончания всех работ. На основе полученных значений ранних и поздних сроков начала и окончания работ выявляется критический путь. После чего вычисляются резервы времени работ и путей. В ряде случаев, помимо определения резервов времени, определяются еще и напряженность сроков выполнения работ путем вычисления коэффициента напряженности, который дает представление о степени важности работ с точки зрения их влияния на срок завершения процесса. Полученные результаты расчетов оформляются в виде таблицы.

В табл. 3 представлены исходные данные и результаты расчета временных параметров работ сетевого графика, изображенного на рис. 17. Обратим внимание на то, что независимые резервы работ (1,2), (2,7) и (4,7) отрицательны, поэтому в табл. 3 они обозначены прочерком (см. параграф 3).

Таблица 3