ТЕМА 3. Булеві функції (Додаткові завдання)

Практичне заняття №3. Булеві функції

 

1. Найдіть висловлення, яким відповідають наступні таблиці істинності:

а)

А

В

С

*

б)

А

В

С

*

в)

А

В

С

*

 

г)

А

В

С

*

д)

А

В

С

*

е)

А

В

С

*

2. За принципом двоїстості побудувати формулу, яка реалізує функцію, двоїсту до :

a) ;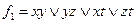

b) ;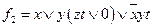

c) ;

d) ;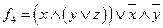

e) ;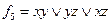

f) .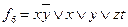

3. Визначте, чи є такі функції самодвоїстими:

a) ;

b) ;

c) ;

d) ;

e) .

4. Перейти від заданої ДНФ до ДДНФ, перетворити ДНФ на КНФ, побудувати ДКНФ:

a) ;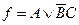

b) ;

c) ;

d) .

5. За допомогою тотожних перетворень побудувати ДДНФ:

a) ;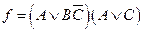

b) ;

c) ;

d) ;

e) .

6. Знайти ДДНФ таких функцій:

a) ;

b) ;

c) .

7. Знайти ДКНФ таких функцій:

a) ;

b) .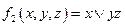

8. Знайти диз’юнктивний розклад функції:

a) ;

b) ;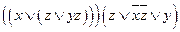

c) ;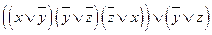

d) ;

e) .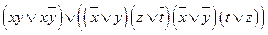

9. Знайти кон’юнктивний розклад функції:

a) ;

b) ;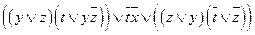

c) ;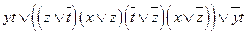

d) ;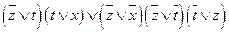

e) ;

f) ;

g) ;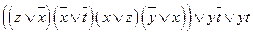

h) ;

i) .

ТЕМА 3. Булеві функції (Додаткові завдання)

 

1. Методом невизначених коефіцієнтів знайти поліном Жегалкіна для функцій:

a) ;

b) ;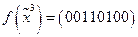

c) .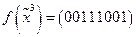

2. За допомогою тотожних перетворень побудувати поліном Жегалкіна для функцій:

a) ;

b) ;

c) .

3. Скориставшись властивістю полінома Жегалкіна, знайти істотні змінні функції:

a) ;

b) ;

c) .

4. Представити у вигляді поліному Жегалкіна логічні функції:

a) ;

b) ;

c) ­ .