Временные параметры сетевых графиков
Одно из важнейших понятий сетевого графика – понятие пути.
Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь 
- любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.
Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, расположенные на этом пути.
В таблице 5.1 приведены основные временные параметры сетевых графиков.
Рассмотрим содержание и расчет указанных параметров.
Таблица 5.1 – Основные временные параметры сетевых графиков
| Элемент сети, характеризуемый параметром | Наименование параметра | Условное обозначение параметра |
| Событие i | Ранний срок свершения события Поздний срок свершения события Резерв времени события |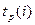 
|
| Работа (i,j) | Продолжительность работы Ранний срок начала работы Ранний срок окончания работы Поздний срок начала работы Поздний срок окончания работы Полный резерв времени работы Свободный резерв времени Независимый резерв времени |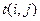 
|
|
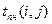
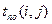
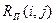
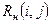
Путь
| Продолжительность пути Продолжительность критического пути Резерв времени пути |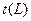 
|
Начнем с параметров событий. Ранний (или ожидаемый) срок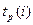 
свершения i-го события – это самый ранний момент времени, к которому завершаются все предшествующие этому событию работы. Счёт времени будем вести от момента наступления начального события. Для удобства расчётов, полагаем, что ранний срок свершения исходного (1-го) события равен нулю (т.е. 
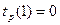). Ранний срок любого последующего события (j-го) определяется продолжительностью самого длительного из предшествующих путей. Отсюда, для определения ранних сроков свершения событий имеем рекуррентное соотношение:
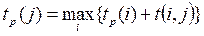. (5.1)
Поздним (или предельным) сроком свершения события i является самый поздний момент времени, после которого остаётся ровно столько времени, сколько необходимо для завершения всех работ, следующих за этим событием. Очевидно, что определяется разностью между продолжительностью критического пути и длиной максимального из последующих путей, начинающихся из события 
. Для событий критического пути ранний и поздний сроки свершения совпадают. Поздний срок находится по формуле, при условии, что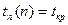 
:
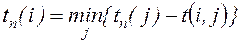. (5.2)
Разность между поздним и ранним сроками свершения события составляет резерв времени i-го события:
. (5.3)
Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическим пути, вызовет такую же задержку в свершении завершающего события.
Из этого следует, что для того чтобы определить длину и топологию критического пути, вовсе не обязательно перебирать все полные пути сетевого графика и определять их длины. Определив ранний срок наступления завершающего события сети, тем самым определяется длина критического пути, выявив события с нулевыми резервами времени, определяется его топология.
Теперь перейдем к параметрам работ.
Отдельная работа может начаться (и окончиться) в ранние, поздние или другие промежуточные сроки.
Очевидно, что ранний срок начала работы (i,j) совпадает с ранним сроком наступления начального (предшествующего) события i, т.е.
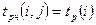. (5.4)
Тогда ранний срок окончания работы (i,j) определяется по формуле
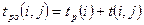. (5.5)
Ни одна работа не может окончиться позже допустимого позднего срока своего конечного события i. Поэтому поздний срок 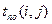окончания работы (i,j) совпадает с поздним сроком свершения её конечного события:
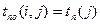, (5.6)
а поздний срок 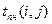начала этой работы равен разности между поздним сроком свершения её конечного события и продолжительностью:
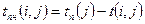. (5.7)
Таким образом, в рамках сетевой модели моменты начала и окончания работы тесно связаны с соседними событиями ограничениями (5.4) – (5.7).
Прежде чем рассматривать резервы времени работ, обратимся к резерву времени пути. Такие резервы имеют все некритические пути. Резерв времени пути определяется как разность между длиной критического и рассматриваемого пути
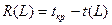. (5.8)
Он показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Если затянуть выполнение работ, лежащих на этом пути, на время большее чем , то критический путь переместится на путь .
Отсюда можно сделать вывод, что любая из работ пути на его участке, не совпадающая с критическим путем (замкнутым между двумя событиями критического пути), обладает резервом времени.
Полный резерв времени 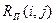работы (i,j) показывает на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв 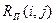определяется по формуле
. (5.9)
Важным свойством полного резерва времени работы является то, что он принадлежит не только этой работе, но и всем полным путям, проходящим через нее. При использовании полного резерва времени только для одной работы резервы времени остальных работ, лежащих на максимальном пути, проходящем через нее, будут полностью исчерпаны. Резервы времени работ, лежащих на других (немаксимальных по длительности) путях, проходящих через эту работу, сократятся соответственно на величину использованного резерва. Все некритические работы имеют полный резерв времени, отличный от нуля.
Свободный резерв времени – это запас времени, которым можно располагать при выполнении данной работы при условии, что начальное и конечное её событие наступят в свои ранние сроки:
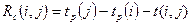. (5.10)
Свободный резерв присущ только данной работе, и его использование никак не повлияет на выполнение последующих работ. Только отдельные работы проекта обладают свободным резервом времени.
Независимый резерв времени 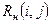работы (i,j) – это часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки:
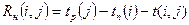. (5.11)
Использование независимого резерва времени не влияет на величину резервов времени других работ. Независимые резервы стремятся использовать тогда, когда окончание предыдущей работы произошло в поздний допустимый срок, а последующие работы хотят выполнить в ранние сроки.
Работы, лежащие на критическом пути, так же как и критические события, резервов времени не имеют.
5.4. Сетевое планирование в условиях неопределенности
При определении временных параметров сетевого графика до сих пор предполагалось, что время выполнения каждой работы точно известно. Однако чаще всего продолжительность работы по сетевому графику заранее не известна и может принимать лишь одно из диапазона возможных значений. Другими словами, продолжительность работы 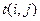является случайной величиной, характеризующейся своим законом распределения, а значит, своими числовыми характеристиками – средним значением, или математическим ожиданием, 
и дисперсией 
.
Практически во всех системах сетевого планирования и управления априори принимается, что распределение продолжительности работ обладает тремя свойствами: а) непрерывностью; б) унимодельностью; в) функция, описывающая распределение, неотрицательна в области неотрицательных значения аргумента.
Кроме того, установлено, что распределение продолжительности работ обладает положительной асимметрией, т.е. максимум кривой смещен влево относительно медианы (линии, делящей площадь под кривой на две равные части). Распределение, как правило, круто поднимается слева от максимального значения 
и полого опускается справа (рис. 5.2).
Простейшим распределением с подобными свойствами является известное в математической статистике распределение Релея:
.
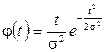Анализ большого количества статистических данных показывает, что это распределение можно использовать в качестве априорного для всех работ.
Рисунок 5.2 – Распределение Релея
Для определения числовых характеристик и этого распределения для работы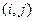 
используют реальные статистические данные о продолжительности работ.
Пусть известны случайные длительности работы 
. Оценку неизвестного параметра 
можно осуществить методом максимума правдоподобия. Для этого необходимо составить функцию правдоподобия
.
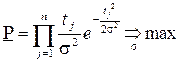Логарифмическая функция правдоподобия имеет вид
Максимизация полученного выражения по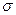 
дает максимально правдоподобную оценку этого параметра. Для этого продифференцируем выражение по 
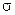и приравняем производную к нулю
.
Отсюда
,
тогда
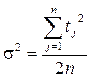. (5.12)
Для распределения Релея известно соотношение между значениями математического ожидания 
и дисперсией :
. (5.13)
Зная и , можно определять временные параметры сетевого графика и оценивать их надежность. Но при этом необходимо учесть, что эти параметры являются средними значениями соответствующих случайных величин: средней длиной критического пути 
, средним значением раннего срока наступления события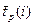 
, средним значением полного резерва времени выполнения работы 
и т.п. Причем, чем больше суммарная дисперсия продолжительности работ критического пути, тем более вероятны значительные по абсолютной величине отклонения.
Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров сети. Весьма важным моментом анализа становится оценка вероятности того, что срок выполнения проекта не превзойдет заданного директивного срока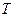 
. Такая вероятность будет равна
.
Если сетевой график включает в себя большое количество работ (более 20), то считают что – случайная величина, имеющая нормальный закон распределения. В этом случае вероятность того, что срок выполнения проекта не превзойдет заданного директивного срока 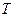, вычисляется следующим образом:
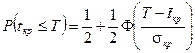. (5.14)
Когда вероятность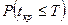 
мала (например, меньше 0,3), то опасность срыва заданного срока выполнения комплекса велика, необходимо принятие дополнительных мер (перераспределения ресурсов по сети, пересмотр состава работ и событий и т.п.). Если 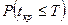значительна (например, более 0,8), то очевидно, с достаточной степенью надежности можно прогнозировать выполнение проекта в установленный срок.