Программируемые логические устройства PLA и PAL (PLD)

СЕМОТЕХНИКА ЭВМ И СИСТЕМ

(Конспект лекций)

ВТОРОЙ МОДУЛЬ

Комплексная цель второго модуля.

Познакомиться с основами структурной и функциональной организации матричных умножителей, БИС/СБИС с программируемой структурой, правилами разработки и оформления схемной документации, выполнить курсовой проект.

ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ ИНТЕГРАЛЬНЫЕ СХЕМЫ

При построении различных цифровых систем могут быть использованы как стандартные так и нестандартные (специализированные) компоненты. К стандартным можно отнести, например, процессор с заданным набором команд, память, к нестандартным – узлы, используемые для управления. Для построения стандартных узлов применяются БИС/СБИС с высокой степенью интеграции. Высокая стоимость проектирования и разработки таких узлов компенсируется большими объемами выпуска и, как следствие, приемлемой ценой микросхем. Реализация нестандартной части раньше чаще всего была связана с использованием ИМС малой и средней степени интеграции, что влекло за собой рост числа корпусов ИМС на плате, усложнение монтажа, снижение надежности системы и ее быстродействия. Заказывать изготовление нестандартных узлов в виде специализированных БИС/СБИС как правило нецелесообразно из-за высокой стоимости проектирования и небольших выпускаемых партий (зачастую это штучный товар). Проблема нашла свое решение с началом выпуска БИС/СБИС с программируемой и репрограммируемой структурой. Первыми представителями этого направления стали программируемые логические матрицы ПЛМ (PLA, Programmable Logic Array), программируемая матричная логика ПМЛ (PAL, Programmable Array Logic) и вентильные матрицы ВМ (GA, Gate Array), чаще называемые базовыми матричными кристаллами БМК. В зарубежной литературе микросхемы PLA и PAL объединяют общим термином SPLD (Simple Programmable Logic Devices) или просто PLD (Programmable Logic Devices). В отечественной литературе они называются программируемыми интегральными логическими схемами (ПЛИС).

Востребованность ПЛМ, ПМЛ, БМК и, как следствие, постоянное развитие этого направления разработки цифровой элементной базы привели к появлению еще более эффективных и совершенных систем, таких как CPLD (Complex Programmable Logic Devices), FPGA (Field Gate Array), SOPC (System On Programmable Chip) и др.

Программируемые логические устройства PLA и PAL (PLD)

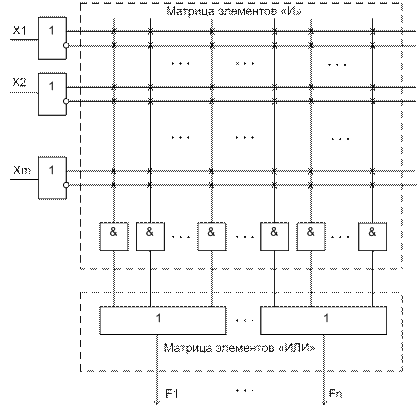
Программируемые логические матрицы ПЛМ (PLA, Programmable Logic Array) являются универсальными логическими схемами, предназначенными для реализации систем логических функций, заданных в дизъюнктивной нормальной форме. ПЛМ состоит из двух программируемых логических матриц (матрицы «И» и матрицы «ИЛИ») и вспомогательных схем, обеспечивающих сопряжение и программирование микросхемы. Представление ПЛМ в виде сочетания матриц “И”, ”ИЛИ” связано с ранним этапом их развития. В настоящее время можно встретить ПЛМ с матрицами других логических элементов. Однако общность представления от этого не страдает, поскольку в итоге функциональные возможности разных схемных вариантов оказываются идентичными. Возможность программировать обе матрицы позволяет подключать любой элемент «И» матрицы «И» к любому элементу «ИЛИ» матрицы «ИЛИ» и это делает ПЛМ более универсальными.

Внутреннюю организацию ПЛМ (PLA) поясняет рисунок, представленный ниже.

Универсальность ПЛМ в части использования любых элементов «И» матрицы «И» с любыми элементами «ИЛИ» матрицы «ИЛИ» становится избыточной при реализации систем логических уравнений с незначительным пересечением друг с другом по одинаковым термам (коньюнкциям). Отказ от такой возможности привел к отказу от программирования матрицы «ИЛИ» и к появлению другой логической структуры, называемой программируемая матричная логика (ПМЛ) PAL - Programmable Array Logic.

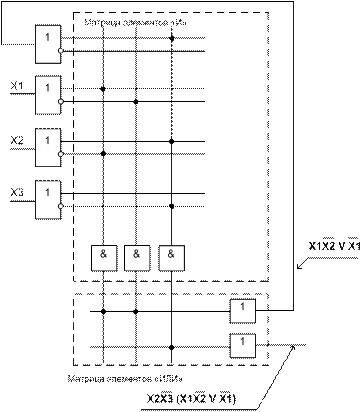
Схемы ПМЛ (PAL) в сравнении с ПЛМ (PLA) более просты в изготовлении и использовании, но имеют меньшую функциональную гибкость, из-за фиксированной матрицы «ИЛИ» и жесткого закрепления элементов «И» за элементами «ИЛИ». Пример такой структуры приведен на следующем рисунке.

Для упрощения схемы многовходовые элементы «И» условно изображены одновходовыми. А возможные точки прожигания отмечены знаками «х». Прожигаются как инверсное так и прямое значение аргумента. Если на пересечении с аргументом Хi точка не запрограммирована, то данный аргумент (переменная) не участвует в формировании коньюнкции.

С помощью ПЛМ или ПМЛ можно реализовывать системы логических уравнений, представленные в дизъюнктивной нормальной форме (ДНФ), в том числе, скобочные формы. Например, схема, представленная ниже, реализует логическое уравнение

 

 

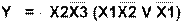
ПЛМ или ПМЛ имеющая s - входов, t – выходов и q – термов (конъюнкции) называется ПЛМ(s,t,q) или ПМЛ(s,t,q). В общем случае с помощью ПЛМ(s,t,q) или ПМЛ (s,t,q) можно реализовать систему из R t логических функций от Н s переменных и I=q различных конъюнкций. Если параметры реализуемой системы логических уравнений не позволяют реализовать ее на одной микросхеме, то возможны следующие три случая:

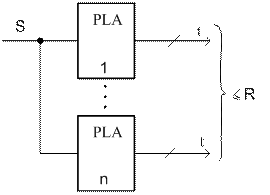
1. Если количество логических функций R>t, необходимо расширить ПЛМ(s,t,q) до ПЛМ(s,R,q). Сделать это можно, соединив n-ПЛМ так как показано на рисунке.

 

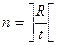
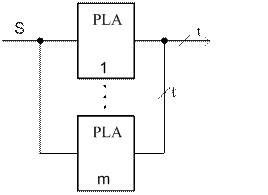
2. Если в реализуемой системе логических уравнений I>q, то необходимо расширить ПЛМ(s,t,q) до ПЛМ(s,t,I), соединив m-ПЛМ по приведенной ниже схеме.

 

 

 

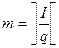
3. Если в реализуемой системе логических уравнений H>s, то необходимо расширить ПЛМ(s,t,q) до ПЛМ(H,t,q). Для этого необходимо использовать специальные декомпозиционные методы синтеза, суть которых сводиться к тому, что сильно связанные переменные закрепляются за отдельными ПЛМ.

Если имеет место комбинация нескольких случаев 1,2,3 то общее количество ПЛМ в схеме будет равно произведению количества ПЛМ для каждого конкретного случая.