Основные теоретические положения
Методические указания
к выполнению лабораторной работы
«Исследование резонанса токов»
Утверждено на заседании
кафедры ЭИКТ
от ..... г. Пр. ...
Сызрань 2010
Составитель: П.П. Гавриш, А.Ю. Карсаков. Ю.А. Мелешкин
УДК 621. 375
ББК 32.85
Исследование резонанса токов: методические указания к лабораторному практикуму по «Общей электротехнике и электронике» / ГОУ ВПО сам ГТУ филиал в г. Сызрани, 2010.
Методические указания предназначены для студентов заочного и дистанционного обучения по специальностям, соответствующим изучению дисциплин «Общая электроника», «Электротехника и электроника», «Теоретические основы электротехники».
Методические рекомендации составлены для проведения лабораторных работ на стендах «ТЭЦ и ОЭ» и 17Д – 03.
Цель работы: ознакомиться с особенностями режимов работы цепи с параллельным соединением активных и реактивных элементов, явлением резонанса токов, повышением коэффициента мощности, применением 1-го закона Кирхгофа в целях переменного тока.
Основные теоретические положения
Рассмотрим электрическую цепь, состоящую из двух параллельных ветвей, схема замещения которой и положительные направления электрических величин приведены на рис. 1
 |
Рис. 1 Схема цепи с двумя параллельными ветвями
Предположим, что цепь присоединена к источнику напряжения  , и определим ток неразветвленного участка цепи, если параметры R1, L, R2, C заданы. Запишем для узла а уравнение по первому закону Кирхгофа
, и определим ток неразветвленного участка цепи, если параметры R1, L, R2, C заданы. Запишем для узла а уравнение по первому закону Кирхгофа  .
.
При синусоидальном напряжении источника токи 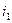 и
и 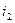 ветвей будут также, синусоидальными, следовательно, синусоидальным будет и ток
ветвей будут также, синусоидальными, следовательно, синусоидальным будет и ток  , поэтому уравнение по первому закону Кирхгофа для мгновенных значений тока можно заменить уравнением для комплексных изображений:
, поэтому уравнение по первому закону Кирхгофа для мгновенных значений тока можно заменить уравнением для комплексных изображений:
 (1)
(1)
Выразим слагаемые уравнения (1) через напряжения, воспользовавшись законом Ома в комплексной форме:
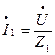 ;
; 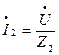 , (2)
, (2)
 и
и 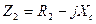 (3)
(3)
Тогда  (4)
(4)
Величину, обратную комплексному сопротивлению, называют комплексной проводимостью и обозначают Y.
Действительную часть комплексной проводимости называют активной проводимостью и обозначают 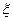 , мнимую часть называют реактивной проводимостью и обозначают в :
, мнимую часть называют реактивной проводимостью и обозначают в :
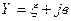 (5)
(5)
Перепишем (4) с учетом того, что:

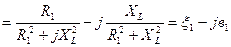 (6)
(6)
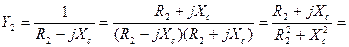
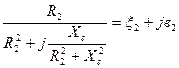 (7)
(7)
Тогда 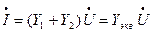 , где
, где  - эквивалентная проводимость цепи.
- эквивалентная проводимость цепи.
Тогда 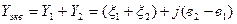 (8)
(8)
где 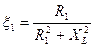 ;
; 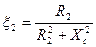 ;
;
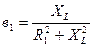 ;
; 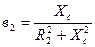 .
.
Эквивалентную комплексную проводимость определяют по правилу, аналогичному правилу для цепей постоянного тока – при параллельном соединении ветвей эквивалентная комплексная проводимость равна сумме комплексных проводимостей ветвей.
Перепишем (8), выразив комплексы проводимостей через комплексы сопротивлений:
 или
или 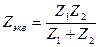 (9)
(9)
Соотношение (9) при известных значениях параметров R1, L, R2, C позволяет определить комплексный ток
 (10)
(10)
и следовательно, найти амплитуду и начальную фазу тока неразветвленного участка цепи.
Анализ фазовых соотношений между током 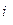 и напряжением U проведем с помощью векторных диаграмм, воспользовавшись понятием активных диаграмм, воспользовавшись понятием активной Ia и реактивной Ip оставляющих тока.
и напряжением U проведем с помощью векторных диаграмм, воспользовавшись понятием активных диаграмм, воспользовавшись понятием активной Ia и реактивной Ip оставляющих тока.
Рассмотрим, например, случай, когда ток 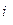 источника отстает по фазе от напряжения U, т.е. угол
источника отстает по фазе от напряжения U, т.е. угол  >0, и обратимся к векторной диаграмме рис. 2
>0, и обратимся к векторной диаграмме рис. 2

Рис 2
На векторной диаграмме осуществлено разложение вектора тока 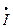 на две взаимно перпендикулярные составляющие
на две взаимно перпендикулярные составляющие 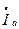 и
и  .
.
Составляющую 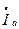 , составляющую по фазе с напряжением U, называют активной составляющей тока или активным током, а составляющую
, составляющую по фазе с напряжением U, называют активной составляющей тока или активным током, а составляющую  , сдвинутую относительно напряжения на угол
, сдвинутую относительно напряжения на угол 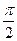 - реактивной составляющей тока или реактивным током. Из векторной диаграммы рис.2 очевидно, что
- реактивной составляющей тока или реактивным током. Из векторной диаграммы рис.2 очевидно, что
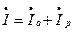 (11)
(11)
и следовательно, 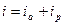 (12)
(12)
где  и
и  - соответственно мгновенные значения активной и реактивной составляющих тока.
- соответственно мгновенные значения активной и реактивной составляющих тока.
Составляющие тока в выражении (11) можно выразить через напряжение и проводимость:
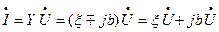 (13)
(13)
Нетрудно видеть, что первое слагаемое в полученном выражении изобразится на комплексной плоскости вектором, параллельным вектору напряжения  , а второе вектором, перпендикулярным вектору напряжения. Следовательно, в соответствии с определением для активной и реактивной соответствующих тока можно записать
, а второе вектором, перпендикулярным вектору напряжения. Следовательно, в соответствии с определением для активной и реактивной соответствующих тока можно записать
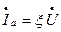 и
и 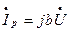 (15)
(15)
 Рассмотрим векторную диаграмму цепи рис. 1, изображенной на рис. 3.
Рассмотрим векторную диаграмму цепи рис. 1, изображенной на рис. 3.
Рис. 3
Рассмотрение диаграммы удобно начинать с вектора напряжения  , который является одним и тем же для обеих параллельных ветвей. Ток первой ветви, содержащей индуктивный элемент, отстает по фазе от напряжения на угол
, который является одним и тем же для обеих параллельных ветвей. Ток первой ветви, содержащей индуктивный элемент, отстает по фазе от напряжения на угол 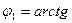
 , соответственно этому расположен на диаграмме изображающий вектор
, соответственно этому расположен на диаграмме изображающий вектор 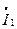 . Ток второй ветви
. Ток второй ветви 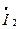 , содержащей емкостной элемент, на некоторый угол
, содержащей емкостной элемент, на некоторый угол 
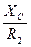 опережает по фазе напряжения. Вектор тока неразветвленного участка
опережает по фазе напряжения. Вектор тока неразветвленного участка 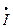 найдем по первому закону Кирхгофа (1). Из простых геометрических построений (к концу вектора
найдем по первому закону Кирхгофа (1). Из простых геометрических построений (к концу вектора 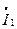 параллельно самому себе присоединяем вектор
параллельно самому себе присоединяем вектор 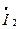 ) получаем вектор тока
) получаем вектор тока 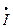 . Очевидно, что модули активной
. Очевидно, что модули активной 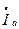 и реактивной
и реактивной  составляющих тока неразветвленного участка цепи связаны с соотношениями
составляющих тока неразветвленного участка цепи связаны с соотношениями  и
и 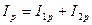 . активные составляющие токов
. активные составляющие токов  ,
,  находятся в фазе, а реактивные
находятся в фазе, а реактивные 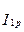 ,
,  - в противофазе.
- в противофазе.
Векторная диаграмма рис. 3 иллюстрирует случай когда 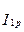 >
>  , поэтому вектор тока неразветвленного участка
, поэтому вектор тока неразветвленного участка 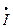 отстает по фазе от вектора напряжения на некоторый угол
отстает по фазе от вектора напряжения на некоторый угол  , при этом говорят, что цепь рис. 1 носит активно-индуктивный характер.
, при этом говорят, что цепь рис. 1 носит активно-индуктивный характер.
 На векторной диаграмме рис. 4 показано, что цепь рис. 1 может носить и ёмкостной характер, т.е. ток неразветвленной цеп может опережать п фазе напряжение, если
На векторной диаграмме рис. 4 показано, что цепь рис. 1 может носить и ёмкостной характер, т.е. ток неразветвленной цеп может опережать п фазе напряжение, если 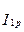 <
<  . такая цепь носит активно-ёмкостной характер.
. такая цепь носит активно-ёмкостной характер.
Рис. 4
 И, наконец, возможен случай, когда между током неразветвленного участка цепи рис. 5 и напряжением нет сдвига по фазе.
И, наконец, возможен случай, когда между током неразветвленного участка цепи рис. 5 и напряжением нет сдвига по фазе.
Рис. 5
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и ёмкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (  ) называют резонансом токов. Резонансу токов соответствует равенство модулей реактивных составляющих токов ветвей:
) называют резонансом токов. Резонансу токов соответствует равенство модулей реактивных составляющих токов ветвей:
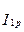 =
=  или
или  . (16)
. (16)
В соответствии с (15)
 (17)
(17)
 ,
,
поэтому учитывая (16) условия резонанса токов можно записать в виде:  (18)
(18)
т.е. в режиме резонанса токов равны модули реактивных проводимостей ветвей, содержащих индуктивные и ёмкостные элементы.
Выразим условия резонанса токов через параметры цепи R1, L, R2, C для чего рассмотрим предварительно векторную диаграмму рис. 3 и запишем соотношения, связывающие модуль тока с модулями его активной и реактивной составляющих. Из треугольников тока, очевидно, что
 и
и  . (19)
. (19)
Следовательно соотношение (16) можно переписать в виде
 (20)
(20)
По закону Ома,
 и
и  , (21)
, (21)
кроме того, в соответствии с рис 6
 |
 ;
;  ;
;  ;
;  ;
;
 ;
;  , (22)
, (22)
 ;
;  .
.
Поэтому учитывая (6), (7), и (21), имеем
 и
и  (23)
(23)
Из (22), (6), (7) имеем:
 ;
;  (24)
(24)
Исходя из условия резонанса токов (18) получаем:
 (25)
(25)
Следует обратить внимание на то, что условия резонанса токов определяются значениями не только токов реактивных, но и активных сопротивлений ветвей:
 (26)
(26)
Или  (26а)
(26а)
Изменением одной из величин (w,L, C, R1,R2,) при остальных четырех постоянных не всегда может быть достигнут резонанс. Резонанс отсутствует, если значение изменяемой величины при ее определении из уравнения (26а) получается мнимым или комплексным. Для L и C могут получаться и по два различных действительных значения, удовлетворяющих уравнению (26а). В таких случаях изменением L и C можно достичь двух различных резонансных режимов.
Решив уравнение (26а) относительно w найдем следующее значение для резонансной угловой частоты:
 , (26б)
, (26б)
где  - резонансная частота при последовательном контуре (резонанс напряжений).
- резонансная частота при последовательном контуре (резонанс напряжений).
 - волновое сопротивление контура.
- волновое сопротивление контура.
Резонанс токов возможен, если сопротивления R1 и R2 оба больше или оба меньше  . Если же это условие не выполнено, получается мнимая частота
. Если же это условие не выполнено, получается мнимая частота  , т.е. не существует такой частоты, которой имел бы место резонанс.
, т.е. не существует такой частоты, которой имел бы место резонанс.
При  резонансная частота
резонансная частота  , т.е. такая же, как и при резонансе в последовательном контуре.
, т.е. такая же, как и при резонансе в последовательном контуре.
При  резонансная частота
резонансная частота  имеет любое значение, т.е. резонанс наблюдается на любой частоте.
имеет любое значение, т.е. резонанс наблюдается на любой частоте.
Действительно при  входное сопротивление контура
входное сопротивление контура
 ,
,
т.е. входное сопротивление контура активно и не зависит от частоты. Следовательно, ток совпадает по фазе с напряжением при любой частоте и его действующее значение равно  .
.
Заметим, что в радиотехнике и электросвязи часто применяются контуры с малыми потерями, т.е. в них R1 и R2 малы по сравнению с  . В таких условиях резонансную частоту можно вычислять по формуле
. В таких условиях резонансную частоту можно вычислять по формуле  .
.
Анализ, который здесь не приводится показывает, что в общем случае сумма энергий электрического и магнитного полей при резонансе не остается постоянной. Эта сумма, т.е. при  .
.
В настоящее время конденсаторы производят, практически без потерь  . Тогда :
. Тогда :
 (27)
(27)
А если и  или
или  <<
<<  , то
, то
 , откуда (28)
, откуда (28)
 ;
;  ;
;  (29)
(29)
и резонанс токов наступает при той же частоте, если парамтры цепи не менять.
Однако создать индуктивность без активных потерь невозможно, так как сопротивление провода :
 (30)
(30)
где  - удельное сопротивление
- удельное сопротивление  ;
;
l – длина провода в М;
S – сечение провода в мм2.
В идеализированном, практически не выполнимом режиме работы, когда  , ток в неразветвленной части равен нулю и входное сопротивление схемы равно бесконечности.
, ток в неразветвленной части равен нулю и входное сопротивление схемы равно бесконечности.
В расположенной цепи фазовые соотношения могут приводить к условиям, невозможным для цепей постоянного тока. так, например, ток неразветвленного участка может быть значительно меньше токов ветвей. Это объясняется тем, что реактивные составляющие токов ветвей 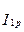 и
и  . находятся в противофазе.
. находятся в противофазе.
Суммирование токов в цепях синусоидального тока следует проводить с учетом фазовых соотношений, т.е. сдвигов по фазе, что осуществляется с помощью комплексных чисел или геометрических построений на комплексной плоскости.
Резонансные кривые
На рис. 7 приведена схема параллельного колебательного контура к которому подключен генератор переменного тока:
 |
 а)
а)
б)
Рис. 7
Через конденсатор проходит ток  , величина которого зависит от напряжения генератора и емкостного сопротивления конденсатора рис. 7.
, величина которого зависит от напряжения генератора и емкостного сопротивления конденсатора рис. 7.
Через катушку проходит ток  , величина которого зависит от напряжения генератора и от индуктивного сопротивления катушки.
, величина которого зависит от напряжения генератора и от индуктивного сопротивления катушки.
Пути обоих токов с учетом фазовых соотношений показаны на рис. 7б.
При резонансе, токи  и
и  сдвинуты между собой по фазе на полпериода, т.е. оказываются взаимно противоположны. Это означает, что результирующий ток
сдвинуты между собой по фазе на полпериода, т.е. оказываются взаимно противоположны. Это означает, что результирующий ток  в общей (неразветвленной) части равен разности токов
в общей (неразветвленной) части равен разности токов  и
и  :
:
 (31)
(31)
Как мы уже знаем при резонансе токи равны  =
=  . При этом ток в общей цепи будет равен нулю.
. При этом ток в общей цепи будет равен нулю.
Ток, проходящий от генератора через идеальный контур (активных потерь нет) при резонансе равен нулю, то сопротивление идеального параллельного контура равно бесконечности (  ).
).
Если иметь в виду реальный контур с активным сопротивлением, то в таком контуре некоторое количество энергии выделяется в активном сопротивлении в виде тепла.
Чтобы амплитуда колебаний не изменялась, от генератора в контур поступает энергия. Иными словами, ток  в общих проводах при наличии в контуре активного сопротивления не равен нулю. Поэтому сопротивление не равно нулю. Поэтому сопротивление реального параллельного контура при резонансе не бесконечно велико, а составляет десятки или сотни кОм.
в общих проводах при наличии в контуре активного сопротивления не равен нулю. Поэтому сопротивление не равно нулю. Поэтому сопротивление реального параллельного контура при резонансе не бесконечно велико, а составляет десятки или сотни кОм.
Величина сопротивления параллельного контура при резонансе определяется по формуле
 ,
,
где  - индуктивность контура – Гн (Генри)
- индуктивность контура – Гн (Генри)
 - ёмкость контура – Ф (Фаради)
- ёмкость контура – Ф (Фаради)
 - активное сопротивление в Омах.
- активное сопротивление в Омах.
Чем больше активные сопротивления R в контуре, тем больше количество энергии расходуется в нем на тепло и тем большее количество энергии поступает от генератора в контур. Следовательно, чем больше активные сопротивление R в контуре, тем больше ток  в общей цепи. Поэтому, чем больше величина активного сопротивления в контуре, тем меньше сопротивления в контуре, тем меньше сопротивление параллельного контура при резонансе.
в общей цепи. Поэтому, чем больше величина активного сопротивления в контуре, тем меньше сопротивления в контуре, тем меньше сопротивление параллельного контура при резонансе.
Проследим теперь зависимость общего тока от частоты генератора. Если частота генератора значительно ниже резонансной частоты контура, то индуктивное сопротивление катушки мало, а емкостное сопротивление конденсатора велико рис. 8. Следовательно,

Рис. 8
04-557.gif">
Рис. 8
ток  велик, а ток
велик, а ток  мал. разность этих токов велика, поэтому ток
мал. разность этих токов велика, поэтому ток  также велик.
также велик.
По мере увеличения частоты генератора (по мере приближения к резонансу) индуктивное сопротивление катушки растет, а ёмкостные сопротивления конденсатора уменьшается. При этом ток  уменьшается, а ток
уменьшается, а ток  растет, разность их уменьшается, а следовательно, уменьшается и общий ток
растет, разность их уменьшается, а следовательно, уменьшается и общий ток  .Контур при более низкой частоте чем резонансная, ведет себя как катушка индуктивности, так как в общей цепи индуктивный ток больше емкостного. При резонансе ток в общей цепи наименьший и контур ведет себя, как активное сопротивление большой величины. При дальнем повышении частоты генератора индуктивное сопротивление продолжает увеличиваться, а ёмкостное – уменьшатся. Ток
.Контур при более низкой частоте чем резонансная, ведет себя как катушка индуктивности, так как в общей цепи индуктивный ток больше емкостного. При резонансе ток в общей цепи наименьший и контур ведет себя, как активное сопротивление большой величины. При дальнем повышении частоты генератора индуктивное сопротивление продолжает увеличиваться, а ёмкостное – уменьшатся. Ток  продолжает уменьшаться, а ток
продолжает уменьшаться, а ток  - увеличивается. Чем выше частота, тем больше разность этих токов, тем больше ток
- увеличивается. Чем выше частота, тем больше разность этих токов, тем больше ток  в общей цепи.
в общей цепи.
При частоте генератора выше резонансной колебательный контур ведет себя как конденсатор, так как емкостной ток больше индуктивного. Зависимость полного сопротивления параллельного контура от частоты показана на рис. 8.
Резонанс напряжений и резонанс токов можно получить ( если  ) и значением частоты генератора при постоянных величинах С и L или изменением резонансной частоты контура. резонансная частота контура изменяется либо изменением индуктивности, либо изменением емкости контура.
) и значением частоты генератора при постоянных величинах С и L или изменением резонансной частоты контура. резонансная частота контура изменяется либо изменением индуктивности, либо изменением емкости контура.