Краткие теоретические сведения

Лабораторная работа №1.2

Исследование электрического резонанса

В Линейной цепи синусоидального тока

Цель работы – изучить резонансные явления при последовательном соединении катушки и конденсатора. В результате проведения лабораторной работы студенты должны знать условия возникновения резонанса, уметь определять параметры колебательного контура: резонансную частоту, характеристическое сопротивление, добротность, затухание, полосу пропускания; приобрести навыки построения графиков частотных характеристик.

Краткие теоретические сведения

В данной работе будем рассматривать последовательную цепь, состоящую из реальной катушки (её обмотка обладает резистивным сопротивлением R) и конденсатора (см. рисунок 1.2.1). Такую цепь часто называют последовательным колебательным (или резонансным) контуром или последовательной RLC-цепью.

 

 

Рисунок. 1.2.1 – Схема исследования резонанса напряжений

Подключение колебательного контура к источнику синусоидального напряжения:

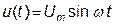(1.2.1)

сопровождается установлением в нём синусоидального, или гармонического, тока:

, (1.2.2)

где u(t) и U_m – соответственно, мгновенное значение и амплитуда напряжения;

i(t)и I_m – соответственно, мгновенное значение и амплитуда тока;

ω – угловая частота [рад/с];

t – время;

φ – угол сдвига фаз между напряжением и током.

Угловую частоту определяют по формуле: 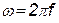, (1.2.3)

а величину сдвига фаз между входным напряжением и током можно рассчитать через параметры элементов цепи: 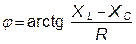, (1.2.4)

где R – активное (резистивное) сопротивление контура.

Величины: 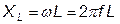и (1.2.5)

называют соответственно индуктивным и ёмкостным сопротивлениями, а их разность:

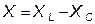(1.2.6)

реактивным сопротивлением цепи.

В частном случае, в цепи с последовательно соединёнными катушкой и конденсатором при равенстве их сопротивлений (X_L=X_C) напряжения на реактивных элементах скомпенсируют друг друга, поэтому такой режим работы этой цепи называют резонансом напряжений.

Режим резонанса в любой цепи наступает, если частота колебаний источника совпадёт с резонансной частотой этой цепи. Для рассматриваемой цепи она определяется по формуле: 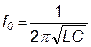, (1.2.7)

Здесь и далее индексом "0" обозначены значения величин при резонансе.

В общем случае, при резонансе в любой цепи её реактивное сопротивление Х=0, напряжение на входе цепи совпадает по фазе с током (j₀=0), и цепь носит чисто активный характер!

Полное сопротивление цепи находится по формуле:

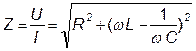. (1.2.8)

На резонансной частоте или, другими словами, в режиме резонанса в последовательной RLC-цепи её полное сопротивление Z минимально (по сравнению с Z на других частотах) и становится равным активному (Z₀=R). В результате ток при резонансе в последовательной RLC-цепи достигает наибольшего значения (по сравнению со значениями тока на других частотах):

. (1.2.9)

Сопротивления реактивных элементов на частоте резонанса:

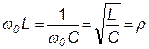, (1.2.10)

Величина ρ — характеристическое сопротивление цепи.

Напряжения на реактивных элементах при их резонансе:

и 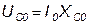(1.2.11)

могут превысить напряжение U на входе рассматриваемой цепи, если активное сопротивление цепи R будет меньше характеристического ρ.

Повышенные значения напряжения на зажимах реактивных элементов, а также тока в цепи, если они не учтены расчетом, могут привести к авариям и вызвать повреждения приборов и аппаратов, находящихся в цепи.

Резонансные свойства колебательного контура также характеризует добротность (качество=quality) контура и затухание .

Для анализа работы цепей, содержащих частотно-зависимые элементы (L и C), часто используют частотные характеристики.

Частотные характеристики – это графики зависимости действующих значений тока, напряжений, а также сдвига фаз и полного сопротивления цепи от частоты. При их построении удобно использовать относительную частоту:

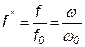, (1.2.12)

Интервал частот f₁ £ f £ f₂, при которых 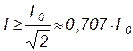(при условии постоянства входного напряжения контура), называют полосой пропускания контура, имея в виду то, что цепь с частотно-зависимыми элементами обладает "избирательными свойствами".

При высокой добротности (Q≥10) полоса пропускания практически симметрична относительно резонансной частоты f₀, и ширина полосы пропускания контура Df находится из условия:

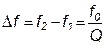или , (1.2.13)

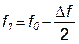где и 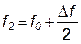, (1.2.14)

соответственно, нижняя и верхняя границы полосы пропускания контура.

Для точного определения характеристик колебательного контура необходимо измерить реальные значения параметров его элементов. Проще всего это выполнить на резонансной частоте f₀. Наличие резонанса устанавливают по максимальному значению токав цепи при неизменном входном напряжении. Измерив частоту f₀, ток I₀ и напряжения U₀, U_K0, U_C0, в соответствии с рисунком 1.2.1, определяют параметры элементов контура:

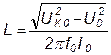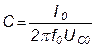, , . (1.2.15)

Фазовый сдвиг между входным напряжением и током в цепи с последовательно соединёнными катушкой и конденсатором определяют по формуле:

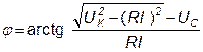. (1.2.16)