Предел суммы двух функций равен
а) сумме пределов слагаемых функций, б) произведению пределов этих функций; в) частному пределов этих функций; г) разности пределов этих функций.
91. Предел отношения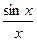 
, при х стремящемся к нулю, равен:
а) cos x, б) 1, в) е, г) 0 .
92. Предел функции 
при х à 3 равен:
а) 1, б) 0, в) -1, г) 1,6.
93. Число, к которому стремится значение функции, когда значение аргумента стремится к конкретному числу х0 называется:
а) производной; б) интегралом; в) пределом функции в точке; г) значением функции в точке.
94. Предел функции в точке равен значению функции в этой точке, если:
а) функция непрерывна в этой точке; б) функция не определена в этой точке;
в) функция монотонна в этой точке; г) функция ограничена в этой точке.
95. Функция называется бесконечно малой в данной точке, если:
а) функция в этой точке равна нулю; б) предел функции в этой точке равен нулю; в) функция ограничена в этой точке; г) функция не определена в этой точке.
96. Функция называется бесконечно большой в данной точке, если:
а) функция в этой точке равна бесконечности; б) предел функции в этой точке равен бесконечности; в) функция не ограничена в этой точке; г) функция не определена в этой точке.
97. Предел функции 3х 2 - 8 при х стремящемся к 2-м равен:
а) 0,5; б) 0, 25; в) 2; г) 4.
98. Производной функции f(x) называется:
а) отношение функции к аргументу, б) предел отношения функции к аргументу,
в) предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0,
г) предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к ∞.
99. Угловой коэффициент прямой у = 2х-3 равен:
а) -3; б) 2; в) 1; г) 5.
100. Угловой коэффициент прямой у = 5-3х равен:
а) -3; б) 2; в) 1; г) 5.
101. Прямая у = 2х+5 образует с положительным направлением оси Oх:
а) острый угол; б) тупой угол; в) прямой угол; г) развернутый угол.
102. Прямая у = -3х+6 образует с положительным направлением оси Oх:
а) острый угол; б) тупой угол; в) прямой угол; г) развернутый угол.