Для студентов второго курса медколледжа

Задания для подготовки к дифференцированному зачету по математике

для студентов второго курса медколледжа

1. Совокупность некоторых объектов, объединенных по какому-либо признаку, называется:

а) множеством, б) перечнем, в) списком, г) объединением.

2. Множество целых чисел обозначается:

а) N, б) Z, в) Q, г) R, д) С.

3. Множество комплексных чисел обозначается:

а) N, б) Z, в) Q, г) R, д) С.

4. Множество натуральных чисел обозначается:

а) N, б) Z, в) Q, г) R, д) С.

5. Множество рациональных чисел обозначается:

а) N, б) Z, в) Q, г) R, д) С.

6. Множество действительных чисел обозначается:а) N, б) Z, в) Q, г) R, д) С.

Дан ряд чисел 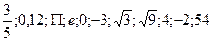. Сколько среди них натуральных чисел?

а) 2 ; б) 3 ; в) 4 ; г) 5.

7. Дан ряд чисел 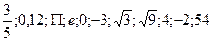. Сколько среди них целых чисел?

а) 7 ; б) 3 ; в) 4 ; г) 5.

8. Дан ряд чисел 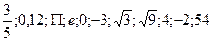. Сколько среди них рациональных чисел?

а) 2 ; б) 3 ; в) 7 ; г) 5.

9. Дан ряд чисел 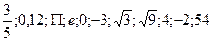. Сколько среди них натуральных чисел?

а) 2 ; б) 3 ; в) 4 ; г) 5.

10. Дан ряд чисел 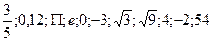. Сколько среди них иррациональных чисел?

а) 2 ; б) 3 ; в) 4 ; г) 5.

11. Дан ряд чисел 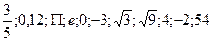. Сколько среди них действительных чисел?

а) 10 ; б) 3 ; в) 4 ; г) 5.

12. Даны два множества: А={а,в,с,d,e,f} и B={n,в,с,r,e,k}. Пересечением этих множеств является множество:

а) {в,с,e,} ; б) {а,в,d,e,f} ; в) {в,с,d,e,f}; г) {n,в,с,r,e,k}.

13. Даны два множества: А={а,в,с,d,e,f} и B={n,в,с,r,e,k}. Объединением этих множеств является множество:

а) {в,с,e,} ; б) {а,в,d,e,f} ; в) {в,с,d,e,f}; г) {а,n,в,d,с,r,e,k,f}.

14. Даны два множества: А={а,в,с,d,e,f} и B={n,в,с,r,e,k}. Разностью множеств А и В является множество:

а) {в,с,e,} ; б) {а,d,f} ; в) {в,с,d,e,f}; г) {а,n,в,d,с,r,e,k,f}.

15. Даны два множества: А={а,в,с,d,e,f} и B={n,в,с,r,e,k}. Разностью множеств В и А является множество:

а) {в,с,e,} ; б) {а,d,f} ; в) {в,с,d,e,f}; г) {n,r,k}.

16. Даны два множества: А={а,в,с,d,e,f} и B={в,с,e}. Множество В вляется:

а) дополнением множества А; б) подмножеством множества А ; в) частью множества А ; г) куском множества А .

17. На координатной оси заданы числовые промежутки А= (1;4), В= [3;7] . Объединением этих множеств будет промежуток:

а) [3,4) ; б) (1,3] ; в) (1,7] ; г) (4,7] .

18. На координатной оси заданы числовые промежутки А= [1;4], В= (3;7) . Объединением этих множеств будет промежуток:

а) [3,4) ; б) (1,7] ; в) [1,7) ; г) (4,7] .

 

19. На координатной оси заданы числовые промежутки А= (1;4), В= [3;7] . Пересечением этих множеств будет промежуток:

а) [3,4) ; б) (1,3] ; в) (1,7] ; г) (4,7] .

20. На координатной оси заданы числовые промежутки А= [1;4], В= (3;7) . Пересечением этих множеств будет промежуток:

а) [3,4) ; б) (1,3] ; в) (1,7] ; г) (3,4] .

21. Дано комплексное число 3 - 4i . Сопряженным ему комплексным числом будет:

а) -3-4i ; б) 4+3i ; в) -3+4i ; г) 3+4i .

22. Дано комплексное число 3 - 4i. Его модуль равен:

а) 5 ; б) 7 ; в) 3 ; г) - 4 .

23. Задана числовая последовательность а_n = 4 n - 3. Пятый член этой последовательности равен:

а) 15, б) 17, в) 18, г) 20

24. Задана числовая последовательность а_n = n² + 1. Третий член этой последовательности равен:

а) 2, б) 1, а) 2, в) 1, г) 10.

25. Числовая последовательность а_n = n² + 1:а) убывающая; б) ограниченная сверху; в) ограниченная; г) ограниченная снизу.

26. Числовая последовательность а_n = - n² + 1:

а) возрастающая; б) ограниченная сверху; в) ограниченная; г) ограниченная снизу.

27. Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d называют:

а) арифметической прогрессией; б) геометрической прогрессией; в) арифметической совокупностью ; г) арифметическим набором.

28. Сумма n первых членов арифметической прогрессии находится по формуле:

а)

б)

в)

г)

29. Известно, что в арифметической прогрессии а₁ = 2, d=2, тогда сумма первых четырех ее членов будет равна:

а) 12, б) 20, в) 14, г) 5.

30. Известно, что в арифметической прогрессии а₁ = 2, d= -2, тогда сумма первых пяти ее членов будет равна:

31. В формуле b_n = b₁ * q ^n-1 число q называют:

а) коэффициентом геометрической прогрессии, б) разностью геометрической прогрессии, в) суммой геометрической прогрессии, г) знаменателем геометрической прогрессии

32. Дана геометрическая прогрессия b₁ , b₂ , b₃ , … b_n . Если b₁ = 2, а q=3, то пятый ее член равен:

а) 50, б) 162, в) 78, г) 180.

 

33. Дана геометрическая прогрессия b₁ , b₂ , b₃ , … b_n . Если b₁ = 2, а q= -3, то пятый ее член равен:

а) -50, б) 162, в) -78, г) 180.

 

34. В формуле общего члена арифметической прогрессии a_n+1 = a_n+ d , где n=1, 2, 3, 4 …, число d называют:

а) коэффициентом арифметической прогрессии, б) разностью арифметической прогрессии, в) суммой арифметической прогрессии, г) знаменателем арифметической прогрессии.

35. Дана арифметическая прогрессия а₁ , а₂ , а₃ , … а_n . Если а₅ = 10, d=2, то первый ее член равен:

а) 5, б) 6, в) 2, г) 8.

 

36. Дана арифметическая прогрессия а₁ , а₂ , а₃ , … а_n . Если а₅ = 10, d= -2,

то первый ее член равен:

а) 15, б) 16, в) 12, г) 18.

 

37. Дана геометрическая прогрессия b₁ , b₂ , b₃ , … b_n . Если b₁ = 2, а q=3,

то b₃ равно:

а) 5, б) 6, в) 7, г) 18.

38. Дана арифметическая прогрессия а₁ , а₂ , а₃ , … а_n . Если а₁ = 1, d=2, то а₄ равно:

а) 5, б) 6, в) 7, г) 8

39. Числовую последовательность, все члены которой отличны от 0 и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют:

а) геометрической последовательностью б) геометрической прогрессией; в) а геометрической совокупностью ; г) геометрическим набором.

40. Сумма n первых членов геометрической прогрессии находится по формуле:

а) 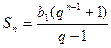б) в)

г) .

41. Дана геометрическая прогрессия b₁ , b₂ , b₃ , … b_n . Если b₃ = 18, а q= -3, то первый ее член равен:

а) -5, б) 2, в) -8, г) 8.

42. Дана геометрическая прогрессия b₁ , b₂ , b₃ , … b_n . Если b₃ =20 , а q= 2, то пятый ее член равен:

а) 5, б) 16, в) 8, г) 18.

 

43. Основное свойство пропорции:

а) сумма крайних членов равна сумме ее средних членов;

б) произведение крайних членов равно произведению ее средних членов;

в) сумма крайних членов равна произведению ее средних членов;

г) произведение крайних членов равно сумме ее средних членов.

44. Неизвестный член х пропорции равен:

а) 4, б) 5, в) 25, г) 50

45. Неизвестный член х пропорции равен:

а) 100, б) 200, в) 20, г) 50

46. Равенство двух кратных отношений называется:

а) прогрессией, б) последовательностью, в) пропорцией, г) множеством

47. Для приготовления раствора лекарственного препарата берут 2 части лекарства и 5 частей воды. Если лекарства взять 20г, то раствора получится:

а) 125г ; б) 70г ; в) 50г ; г) 120г.

48. Для приготовления 20%-го раствора лекарственного препарата лекарства и воды необходимо взять в соотношении:

а) 2 : 5; б) 1 : 5; в) 2 : 3; г) 1 : 4.

49. Есть два числа: 20 и 30. Второе число больше первого на:

а) 100 % ; б) 150 % ; в) 50 % ; г) 200% .

50. Есть два числа: 10 и 40. Первое число меньше второго на:

а) 100 % ; б) 150 % ; в) 75 % ; г) 200% .

51. Чтобы приготовить 9% раствор из расчета на 1 литр, необходимо взять сухого вещества:

а) 90 г; б) 180г; в) 9г; г) 200г .

52. Зная разовую дозу (0,3г), и, зная, что больной принимает лекарство десертными ложками, процентная концентрация раствора будет:

а) 3%; б) 30%; в) 6% ; г) 33%.

53. Если больной должен принимать жидкое лекарственное вещество по 1 чайной ложке 4 раза в день 7 дней, то ему необходимо выписать следующее количество раствора:

а) 250 мл; б) 300 мл; в) 200 мл; г) 100мл.

54. Для приготовления лечебной мази смешивают лекарственные препараты в соотношении 2:3:5. Если наименьшего лекарства взять 30г, то мази будет получено:

а) 100г ; б)200г; в) 150г ; г) 250г.

55. Минимальная масса доношенного ребенка 2500г. Прибавка веса ребенка в 600 г за первый месяц жизни составит:

а) 10%, б) 24%, в) 25%, г) 50%

56. Согласно калорийному методу в последнюю четверть года на 1 кг массы тела ребенка в сутки полагается 100 ккал. Если 1 литр содержит 700 ккал, а масса тела ребенка в 9 месяцев составила 7 кг, то количество грудного молока, необходимого ребенку в сутки равно:

а) 500 г, б) 700 г, в) 900 г, г) 1000 г

57. Минимальная длина тела доношенного новорожденного 45 см. Прибавка длины тела на 9 см за первые три месяца жизни составит от роста ребенка:

а) 10%, б) 20%, в) 25%, г) 50%

58. Согласно объемному методу расчета суточного рациона здорового малыша в возрасте от 2 до 6 недель объем питания должен составлять пятую часть массы тела. Тогда суточный объем питания при массе тела 4000 г должен быть равен:

а) 600г, б) 800г, в) 900г, г) 1000г

59. Суточное количество пищи ребенка в возрасте 4-6 лет должно составлять 90 ккал на 1кг веса. Тогда суточное количество пищи для ребенка весом 9кг 300 г должно быть равно:

а) 1037, б) 837, в) 850, г) 945

60. Функцией y=f(x) называется:

а) множество значений аргумента х, б) соответствие, при котором каждому значению аргумента х соответствует одно и только одно значение функции у, в) числовая последовательность значений функции у; г) числовая последовательностению аргумента х соответствует одно и только одно значение функции у, в) числовая последовательность значений функции у; г) числовая последовательность значений аргумента х.

61. E(f) – обозначается:

а) область определения функции f(x), б) множество значений функции f(x); в) множество допустимых значений аргумента х; г) множество допустимых значений функции у.

62. Способ задания функции в виде :

х	у

 

называется: а) табличным, б) аналитическим, в) графическим, г) словесным.