Исследование знака корней квадратного уравнения
Рассмотрим такую задачу. Дано квадратное уравнение с параметром, нужно провести полное исследование знаков корней уравнения в зависимости от значений параметра. Здесь применяются два подхода: решение уравнения и использование формул Виета. Если дискриминант уравнения является полным квадратом, а старший коэффициент не зависит от параметра, то проще решить уравнение и исследовать знаки корней непосредственно.
1. Определить знаки корней уравнения 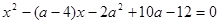 в зависимости от параметра. Решение. Найдем дискриминант
в зависимости от параметра. Решение. Найдем дискриминант 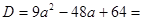
 . Поскольку дискриминант является полным квадратом, то несложно решить это уравнение:
. Поскольку дискриминант является полным квадратом, то несложно решить это уравнение: 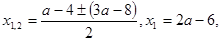
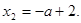 Оба корня положительны, если
Оба корня положительны, если  . Оба корня отрицательны, если
. Оба корня отрицательны, если 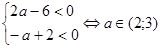 . Проверяем остальные промежутки: при
. Проверяем остальные промежутки: при 
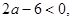
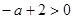 , при
, при 
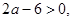
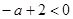 , т. е. корни имеют разные знаки. В оставшихся точках, при
, т. е. корни имеют разные знаки. В оставшихся точках, при 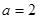 ,
,  корни вычисляем: один корень равен нулю, а второй отрицательный. Нужно еще отметить, когда корни совпадают:
корни вычисляем: один корень равен нулю, а второй отрицательный. Нужно еще отметить, когда корни совпадают: 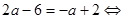
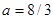 , при этом кратный корень равен
, при этом кратный корень равен 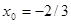 . Задача решена, но полезно рассмотреть геометрическую иллюстрацию. Изобразим на плоскости AОX прямые
. Задача решена, но полезно рассмотреть геометрическую иллюстрацию. Изобразим на плоскости AОX прямые 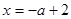 и
и  (рис. 1). Всю информацию о знаках корней при различных значениях
(рис. 1). Всю информацию о знаках корней при различных значениях  мы можем прочитать по чертежу: для данного значения
мы можем прочитать по чертежу: для данного значения  мысленно проведем вертикальную прямую и отметим точки пересечения с прямыми
мысленно проведем вертикальную прямую и отметим точки пересечения с прямыми 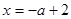 и
и  , их ординаты и являются корнями уравнения. По чертежу хорошо видно, что при
, их ординаты и являются корнями уравнения. По чертежу хорошо видно, что при  и при
и при 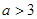 один корень отрицательный, а другой положительный, при
один корень отрицательный, а другой положительный, при 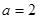 и при
и при  — один отрицательный, а другой равен нулю, при
— один отрицательный, а другой равен нулю, при 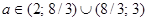 два различных отрицательных корня, а при
два различных отрицательных корня, а при 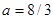 — кратный отрицательный корень. Ответ: при
— кратный отрицательный корень. Ответ: при  и при
и при 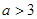 корни разных знаков, при
корни разных знаков, при 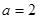 и при
и при  один корень отрицательный, а другой равен нулю, при
один корень отрицательный, а другой равен нулю, при 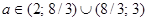 два различных отрицательных корня, при
два различных отрицательных корня, при 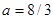 кратный отрицательный корень.
кратный отрицательный корень.
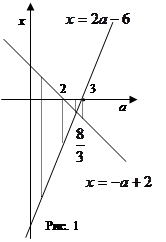 Если же корни уравнения — иррациональные выражения, то непосредственное исследование их знака будет слишком громоздким. Поэтому исследование проводят с помощью формул Виета. Приведем схему такого исследования.
Если же корни уравнения — иррациональные выражения, то непосредственное исследование их знака будет слишком громоздким. Поэтому исследование проводят с помощью формул Виета. Приведем схему такого исследования.
1) Если старший коэффициент зависит от параметра, то находим, при каких значениях параметра он равен нулю. Подставляем эти значения в уравнение и решаем полученное линейное уравнение. Определяем знак его корня.
2) Находим дискриминант уравнения и решаем неравенство 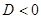 . Таким образом, выясняем, при каких значениях параметра корней нет.
. Таким образом, выясняем, при каких значениях параметра корней нет.
3) Рассмотрим значения параметра, при которых 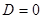 , т. е. корни совпадают. Нужно их найти и определить знак.
, т. е. корни совпадают. Нужно их найти и определить знак.
4) Рассмотрим значения параметра, при которых  . Оба корня положительны тогда и только тогда, когда их сумма и произведение положительны. Оба корня отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно. Корни имеют разные знаки тогда и только тогда, когда их произведение отрицательно. Используя формулы Виета, составляем и решаем соответствующие системы.
. Оба корня положительны тогда и только тогда, когда их сумма и произведение положительны. Оба корня отрицательны тогда и только тогда, когда их сумма отрицательна, а произведение положительно. Корни имеют разные знаки тогда и только тогда, когда их произведение отрицательно. Используя формулы Виета, составляем и решаем соответствующие системы.
5) Отдельно надо разобрать случай, когда один из корней равен нулю. Для этого подставляем 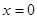 в уравнение, находим значение параметра и второй корень.
в уравнение, находим значение параметра и второй корень.
Чаще в задачах нужна только часть такого исследования.
2. При каких значениях параметра  уравнение
уравнение 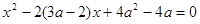 имеет два различных положительных корня? Решение. Оба корня положительны тогда и только тогда, когда их сумма и произведение положительны. Чтобы корни существовали и были различны, потребуем, чтобы дискриминант был положителен. Получим систему
имеет два различных положительных корня? Решение. Оба корня положительны тогда и только тогда, когда их сумма и произведение положительны. Чтобы корни существовали и были различны, потребуем, чтобы дискриминант был положителен. Получим систему 
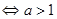 . Ответ:
. Ответ:  .
.
3. При каких значениях  уравнение
уравнение 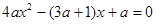 не имеет положительных корней? Решение. При
не имеет положительных корней? Решение. При 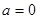 получаем
получаем 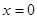 , положительных корней нет. Найдем дискриминант уравнения
, положительных корней нет. Найдем дискриминант уравнения 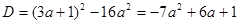 . Значит, при
. Значит, при  уравнение не имеет никаких корней. Чтобы оба корня были отрицательны, необходимо и достаточно, чтобы выполнялись условия: сумма корней
уравнение не имеет никаких корней. Чтобы оба корня были отрицательны, необходимо и достаточно, чтобы выполнялись условия: сумма корней  , а произведение корней
, а произведение корней  . Составим систему
. Составим систему 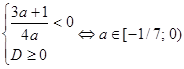 . Если один корень равен 0, то
. Если один корень равен 0, то 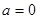 и других корней нет. Значит, нужно объединить промежутки
и других корней нет. Значит, нужно объединить промежутки 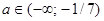
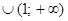 , где нет никаких корней, промежуток
, где нет никаких корней, промежуток 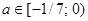 , где оба корня отрицательны, и точку 0, где один нулевой корень. Ответ:
, где оба корня отрицательны, и точку 0, где один нулевой корень. Ответ: 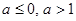 .
.
4. Определить знак корней квадратного уравнения 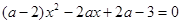 . Решение.1) Рассмотрим случай
. Решение.1) Рассмотрим случай 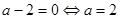 . В этом случае получаем линейное уравнение
. В этом случае получаем линейное уравнение 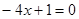 , т. е. в этом случае имеется один положительный корень. 2) Пусть
, т. е. в этом случае имеется один положительный корень. 2) Пусть 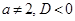 . Так как
. Так как 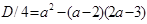
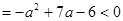 , то при
, то при 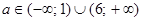 корней нет. 3) При
корней нет. 3) При 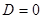
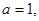
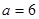 , получаем уравнение
, получаем уравнение  с отрицательным корнем
с отрицательным корнем 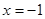 и уравнение
и уравнение  с положительным корнем
с положительным корнем 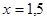 . 4) Пусть
. 4) Пусть  . Оба корня положительны, если
. Оба корня положительны, если 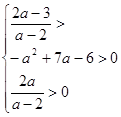
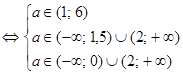
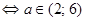 . Оба корня отрицательны, если выполняются условия
. Оба корня отрицательны, если выполняются условия 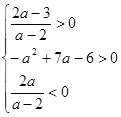

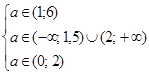
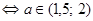 . Корни разных знаков, если
. Корни разных знаков, если 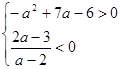
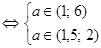
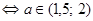 . 6) Пусть один корень равен нулю. Подставляя
. 6) Пусть один корень равен нулю. Подставляя 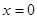 в уравнение, получаем
в уравнение, получаем  . Само уравнение приобретает вид
. Само уравнение приобретает вид  . Значит, второй корень отрицательный. Ответ: при
. Значит, второй корень отрицательный. Ответ: при 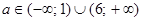 корней нет, при
корней нет, при  отрицательные корни, при
отрицательные корни, при  один корень отрицательный, второй равен нулю, при
один корень отрицательный, второй равен нулю, при  корни разных знаков, при
корни разных знаков, при  корни положительны.
корни положительны.