ОСТАТОЧНОЕ ВРЕМЯ ЖИЗНИ

 

При страховании жизни страхователь имеет дело с конкретными людьми, уже дожившими до определенного возраста x. Поэтому необходимо рассмотрение случайной величины

 

, (7)

 

определяющей остаточное время жизни человека, дожившего до х лет.

Закон распределения вероятностей этой случайной величины можно задать как . Эту вероятность в страховой математике принято обозначать как :

- (8)

вероятность смерти человека, достигшего возраста x лет, в течение ближайших t лет.

Дополнительная вероятность обозначается как :

-

это вероятность того, что человек в возрасте x лет проживет еще не менее лет.

В частном случае, при индекс опускают:

 

 

вероятность того, что человек в возрасте х лет умрет в течение ближайшего года, и

 

вероятность того, что человек в возрасте х лет проживет, по крайней мере, еще один год.

Через эти характеристики можно выразить и вероятности :

;

 

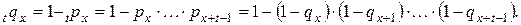
Рассматривается также и вероятность

того, что человек в возрасте x лет проживет еще t лет, но умрет на протяжении последующих u лет. Эта вероятность будет вычисляться как

или

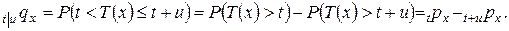
Учитывая формулу (8) можем получить:

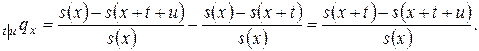(9)

Если , то

-

вероятность того, что человек в возрасте x лет проживет еще t лет, но умрет на протяжении следующего года.

 

№ 1. Используя Приложение вычислить вероятность того, что человек в возрасте 40 лет:

а) проживет, по крайней мере, еще 3 года;

б) проживет еще 3 года, но умрет на протяжении следующего года;

в) проживет еще 3 года, но умрет на протяжении последующих 2 лет.

Решение.

а) Так как , , то

 

;

б) ;

 

в) .

 

Ответ: а) 0,98949; б) 0,00389; в) 0,00799.