Доказательство.

П. 8. Основные теоремы дифференциального исчисления

Теорема Ферма (Пьер Ферма, француз, 1601–1665 г.р.)

Пусть функция 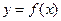определена на интервале и в некоторой точке принимает наибольшее или наименьшее значение. Тогда, если в точке х₀ существует конечная производная, то она равна нулю:

Доказательство.

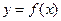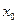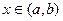Пусть функция в точке принимает наибольшее значение, т.е. для любой точки . Это означает, что для любой точки справедливо неравенство .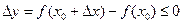

Тогда, если 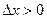, т.е. x > x₀, то ,

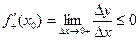если 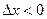, т.е. x < x₀, то

По условию теоремы производная в точке х₀ существует. Это возможно лишь в том случае, когда справедливо равенство 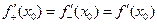, при этом получили, что 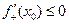, , т.е. равенство будет справедливо лишь в одном случае, когда .

(что и требовалось доказать)

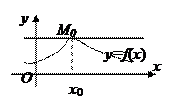Замечания.

1.Геометрический смысл теоремы: касательная к графику функции 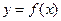в точке M(x₀,f(x₀)) параллельна оси (Ох).

 

 

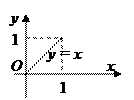
2. Нельзя в формулировке теоремы рассматривать не интервал , а отрезок .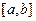

Например, рассмотрим функцию на отрезке [0,1]. На нем функция принимает наименьшее значение y = 0 в точке х = 0, а наибольшее y = 1 в точке х = 1. Но 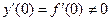и , так как 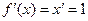для всех х.