Решение неравенств методом интервалов
В основе метода интервалов лежит следующее свойство двучлена  : точка
: точка  делит числовую ось на две части − справа от точки
делит числовую ось на две части − справа от точки  двучлен
двучлен  , а слева от точки
, а слева от точки  .
.
Пусть требуется решить неравенство  , где
, где  – фиксированные числа, среди которых нет равных, причем такие, что
– фиксированные числа, среди которых нет равных, причем такие, что  .
.
Для решения неравенства  методом интервалов поступают следующим образом: на числовую ось наносят числа
методом интервалов поступают следующим образом: на числовую ось наносят числа  в промежутке справа от наибольшего из них, то есть числа
в промежутке справа от наибольшего из них, то есть числа  , ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем – знак «плюс», затем знак «минус».
, ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем – знак «плюс», затем знак «минус».
Тогда множеством всех решений неравенства  является объединение всех промежутков, в которых поставлен знак «плюс».
является объединение всех промежутков, в которых поставлен знак «плюс».
Множеством решений неравенства 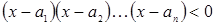 является объединение всех промежутков, в которых поставлен знак «минус».
является объединение всех промежутков, в которых поставлен знак «минус».
Решение рациональных неравенств (то есть неравенств вида  ,
,  ,
,  ,
, 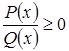 ,
,  ,
,  и др., где
и др., где 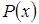 и
и  – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках
– многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках  и
и 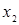 , и, между этими точками, не имеет других корней, то в промежутках
, и, между этими точками, не имеет других корней, то в промежутках 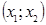 функция сохраняет свой знак.
функция сохраняет свой знак.
Поэтому для нахождения промежутков знакопостоянства функции  на числовой оси отмечают все точки, в которых функция
на числовой оси отмечают все точки, в которых функция  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Эти точки разбивают числовую ось на несколько промежутков, внутри каждого из которых функция  непрерывна и не обращается в нуль, то есть сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой оси.
непрерывна и не обращается в нуль, то есть сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой оси.
Для определения интервалов знакопостоянства рациональной функции, то есть для решения рационального неравенства, отмечают на числовой оси корни числителя и корни знаменателя, которые являются корнями и точками разрыва соответствующей функции.
Для решения неравенств вида  , где
, где  числовую ось разбивают на промежутки
числовую ось разбивают на промежутки  .
.
На каждом из этих промежутков исходное неравенство имеет постоянный знак. Поэтому достаточно узнать знак выражения в одной из точек промежутка, чтобы узнать его на всем промежутке. Определив знак выражения, выбираем те промежутки, на которых это выражение положительно. Объединение положительных промежутков и является множеством решений неравенства.

 .
.
Пример. Решим неравенство 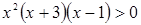 .
.
Решение. Расположим на числовой оси корни многочлена, стоящего в левой части неравенства.

При 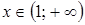 многочлен положителен, так как все множители, стоящие в левой части положительны. Двигаясь по оси
многочлен положителен, так как все множители, стоящие в левой части положительны. Двигаясь по оси  справа налево при переходе через точку
справа налево при переходе через точку  , многочлен меняет знак и становится отрицательным. При переходе через точку
, многочлен меняет знак и становится отрицательным. При переходе через точку 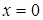 многочлен не меняет знак. При переходе через точку
многочлен не меняет знак. При переходе через точку 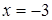 многочлен опять меняет знак и становится положительным. Решением неравенства является все
многочлен опять меняет знак и становится положительным. Решением неравенства является все  .
.
Решение рациональных неравенств вида 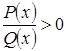
 , где
, где 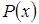 и
и  – многочлен, сводится к решению равносильного неравенства
– многочлен, сводится к решению равносильного неравенства 
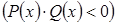 , полученного из данного неравенства умножением обеих частей неравенства на многочлен
, полученного из данного неравенства умножением обеих частей неравенства на многочлен  , который положителен при всех допустимых значениях неизвестного (то есть при
, который положителен при всех допустимых значениях неизвестного (то есть при  , для которых
, для которых  .)
.)
Пример. Для решения неравенства 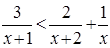 перенесем все слагаемые в левую часть и, приводя к общему знаменателю, получим равносильное неравенство
перенесем все слагаемые в левую часть и, приводя к общему знаменателю, получим равносильное неравенство 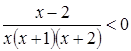 равносильное неравенству
равносильное неравенству  .
.
Используя метод интервалов, имеем:

С помощью «пробных» точек найдем знак выражения в каждом промежутке. В интервалах  выполняется неравенство.
выполняется неравенство.
Ответ. 
Множеством решений нестрогих неравенств  и
и  является объединением всех решений строго неравенства
является объединением всех решений строго неравенства  и множества всех решений уравнения
и множества всех решений уравнения  , а множеством решений нестрого неравенства вида
, а множеством решений нестрого неравенства вида  является объединением множества всех решений неравенства
является объединением множества всех решений неравенства  и множества всех решений уравнения
и множества всех решений уравнения  .
.
Пример. Решим неравенство  .
.
Решение. Область определения данного неравенства  ,
, 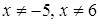 .
.
С учетом области допустимых значений данное неравенство равносильно неравенству  , множество решений которого находим, объединив множество решений неравенства
, множество решений которого находим, объединив множество решений неравенства  и множество решений уравнения
и множество решений уравнения  . Нанесем числа, при которых числитель и знаменатель обращаются в нуль на числовую ось, и которые разбивают числовую ось на пять промежутков:
. Нанесем числа, при которых числитель и знаменатель обращаются в нуль на числовую ось, и которые разбивают числовую ось на пять промежутков:

Принимая во внимание область определения исходного неравенства, находим множество его решений:  .
.
Ответ.  .
.
Пример. Решим дробно-линейное неравенство, указав его целые решения:  .
.
Решение. Неравенство  равносильно совокупности двух линейных систем неравенств:
равносильно совокупности двух линейных систем неравенств:

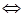
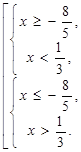


 .
.
Система (2) не имеет решений. Следовательно,, решением неравенства  является
является  . Целые решения неравенства:
. Целые решения неравенства:  .
.
Ответ. Целые решения неравенства:  .
.