Постановка транспортной задачи по критерию стоимости.

Транспортная задача.

Транспортная задача — задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пунк­та производства (станций отправления) в пункты потребления (станции назначения) — является важнейшей частной задачей ли­нейного программирования, имеющей обширные практические при­ложения не только к проблемам транспорта.

Транспортная задача выделяется в линейном программирова­нии определенностью экономической характеристики, особенностя­ми математической модели, наличием специфических методов ре­шения.

Простейшая формулировка транспортной задачи по критерию стоимости следующая: в т пунктах отправления на­ходится соответственно единиц однородного груза (ре­сурсы), который должен быть доставлен n потребителям 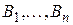в количествах единиц (потребности). Известны транспорт­ные издержки перевозок единицы груза из 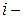го пункта отправ­ления в й пункт потребления.

Требуется составить план перевозок, т. е. найти, сколько еди­ниц груза должно быть отправлено из 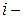го пункта отправления в й пункт потребления так, чтобы полностью удовлетворить по­требности и чтобы суммарные издержки на перевозки были мини­мальными.

Для наглядности условия транспортной задачи представим в виде таблицы, которая называется распределительной.

 

Поставщик Потребитель   Запас груза
…
    …  
… … … … …
    …  
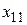
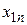
  Потребность в грузе     …    

 

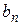
Здесь количество груза, перевозимого из 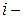го пункта отправления в й пункт назначения, равно , запас груза в 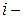м пункте отправ­ления определяется величиной 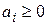, а потребность го пункта назначения в грузе равна . Предполагается, что все .

Матрица называется матрицей тарифов (издержек или транспортных расходов).

Планом транспортной задачи называется матрица , где каждое число обозначает количество единиц груза, которое надо доставить из 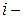го пункта отправления в й пункт назначения. Матрицу называют матрицей перевозок.

Общие суммарные затраты, связанные с реализацией плана перевозок, можно представить целевой функцией

(1).

Переменные должны удовлетворять ограничениям по запа­сам, по потребителям и условиям неотрицательности:

– ограничения по запасам (2);

– ограничения по потребителям (2);

– условия неотрицательности (3).

Таким образом, математически транспортная задача формули­руется следующим образом. Даны система ограничений (2) при условии (3) и целевая функция (1). Требуется среди множества решений системы (2) найти такое неотрицательное решение, ко­торое минимизирует функцию (1).

Система ограничений задачи (1) – (3) содержит уравнений с тп переменными. Предполагается, что суммарные за­пасы равны суммарным потребностям, т. е.

(4).

 

Признак разрешимости транспортной задачи.

Для того чтобы транспортная задача имела до­пустимые планы, необходимо и достаточно выполнения равен­ства

.

Различают два типа транспортных задач: закрытые, в кото­рых суммарный объем груза поставщиков равен суммарному спро­су потребителей, т.е.

и открытые, в которых суммарная производственная мощность по­ставщиков превышает спрос потребителей или спрос потребителей больше фактической суммарной мощности поставщиков, т. е.

или .

Открытую модель можно преобразовать в закрытую. Так, если , то в математическую модель транспортной задачи вводится фиктивный -й пункт назначения. Для этого в мат­рице задачи предусматривается дополнительный столбец, для которого потребность равна разности между суммарной мощностью по­ставщиков и фактическим спросом потребителей:

.

Все тарифы на доставку груза в этот пункт будем считать равны­ми нулю. Этим самым открытая модель задачи преобразуется в закрытую. Для новой задачи целевая функция всегда одна и та же, так как цены на дополнительные перевозки равны нулю. Ины­ми словами, фиктивный потребитель не нарушает совместности системы ограничений.

Если же , то вводится фиктивный -й пункт отправления, которому приписывают запас груза, равный

.

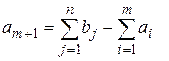Тарифы на доставку грузов от этого фиктивного поставщика опять полагаем равными нулю. В матрице добавится одна строка, на целевую функцию это не повлияет, а система ограничений за­дачи станет совместной, т. е. станет возможным отыскание опти­мального плана.

Для транспортной задачи важное значение имеет следующая теорема.

Теорема. Ранг матрицы транспортной задачи на единицу меньше числа уравнений, т. е. .

Из теоремы следует, что каждый опорный план должен иметь 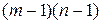свободных пере­менных, равных нулю, и 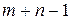базисных переменных.

План перевозок транспортной задачи будем отыскивать непо­средственно в распределительной таблице. Примем, что если переменная принимает значение , то в соот­ветствующую клетку 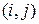будем записывать это значение, если же , то клетку 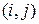оставим свободной. С учетом теоремы о ранге матрицы в распределительной таблице опорный план должен содержать 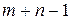занятых клеток, а остальные будут свободные.

Указанные требования к опорному плану не являются единст­венными. Опорные планы должны удовлетворять еще одному тре­бованию, связанному с циклами.

Набор клеток матрицы перевозок, в котором две и только две соседние клетки расположены в одной строке или в одном столбце и последняя клетка набора лежит в той же строке или столбце, что и первая, называется замкнутым циклом.

Графически цикл представляет собой замкнутую ломаную линию, вершины которой расположены в занятых клетках таблицы, а звенья расположены только в строках или столбцах. При этом в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое в столбце. Если ломаная линия, образующая цикл, пересекает саму себя, то точки самопересечения не являются вершинами.

С набором клеток цикла связаны следующие важные свойства планов транспортной задачи:

1) допустимый план транспортной задачи является опорным тогда и только тогда, когда из занятых этим планом клеток нельзя образовать ни одного цикла;

2) если имеем опорный план, то для каждой свободной клетки можно об­разовать только один цикл, содержащий данную клет­ку и некоторую часть занятых клеток.

5.2 Построение исходного опорного плана