ПРОЦЕССЫ ИДЕАЛЬНОГО ГАЗА.
4.1 ИЗОХОРНЫЙ ПРОЦЕСС: V=const.
Из уравнения Клайперона для двух произвольных состояний изохорного процесса:
; 
(4.1)
При постоянном объеме V=const давления одинаковых масс одного и того же газа относятся как абсолютные температуры (закон Шарля).
Δ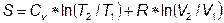 
т.к. 
следовательно:
Δ 
; Δ 
(4.2)
Iый закон термодинамики для изохорного процесса:
dq=du, так как P*dV=0
q= 
; du= (4.3)
величина внутренней энергии газа зависит только от ΔT.
ИЗОБАРНЫЙ ПРОЦЕСС: Р=const.
Из уравнения Клайперона для двух произвольных состояний изобарного процесса:
;
(4.5)
При постоянном давлении Р=const объемы одинаковых масс одного и того же газа относятся как абсолютные температуры (закон Гей-Люссака).
Для энтропии:
; 
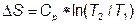(4.6)
; 
(4.7)
Iый закон термодинамики для изобарного процесса:
= 
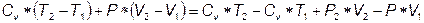
так как 
(4.8)
4.2. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС: T=const.
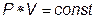- изотерма в координатах P, V представляет собой гиперболу (закон Бойля- Мариотта).
Из уравнения Клайперона для двух произвольных состояний изотермического процесса:
; 
; 
(4.9)
Так как внутренняя энергия идеального газа зависит только от температуры, то в изотермическом процессе внутренняя энергия не изменяется.
; du=0 и следовательно
dq=dL; q=L (4.10)
Теплоту и работу изотермического процесса, совершенного идеальным газом, рассчитывают по формуле, полученной методами высшей математики:
(4.11)
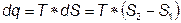(4.12)
4.3.АДИАБАТНЫЙ ПРОЦЕСС: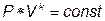 
; q=0.
; 
; S=const
| |
Процесс без подвода и отвода теплоты к рабочему телу q=0; P=varia; V=varia; T=varia .
уравнение адиабаты (Пуассона).
Аналитическое выражение Iго закона термодинамики для адиабатного процесса:
; 
; 
Отсюда видно, что работа выполняется в результате изменения внутренней энергии.
; 
(**)
Используя уравнение 
и поделив на Т (**) запишем:
(***)
Зная, что 
получим, поделив его и уравнение (***) на Сv:
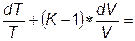0
Проинтегрируем это уравнение, считая K=const:
, зависимость между T и V; (4.13)
, зависимость между Р и V; (4.14)
, зависимость между Р и 
; (4.15)
, зависимость между Р и Т (4.16)
Работа 1 кг газа определяется по следующим формулам:
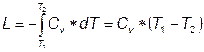(4.17)
либо
; 
;
(4.18)
(4.19)
; 
(4.20)
; 
Так как в адиабатном процессе dq=0, то С= 
.