Примеры расчета магнитных цепей
Пример 4.1. Расчет неразветвленной неоднородной магнитной цепи постоянного тока.
Задание:
1. Вычислить ток I в катушке, необходимый для создания заданного магнитного потока Фdв максимальном воздушном зазоре магнитной цепи dmax (рис.4.1) и определить индуктивность катушки L.
2. Определить величину магнитного потокаФ при отсутствии воздушного зазора и токе катушки, рассчитанном в п. 1.
3. Построить тяговую характеристику электромагнита при токе катушки, рассчитанном в п. 1.
Потоками рассеивания и полями выпучивания пренебречь.
|


|
Рис.4.1
Решение:
Алгоритм расчета неразветвленной неоднородной магнитной цепи постоянного тока, изображенной на рис.4.1 содержит несколько этапов.
На первом этапе, для определения силы тока, решается прямая задача расчета магнитной цепи. По значению магнитного потока Ф и известным геометрическим параметрам элементов магнитопровода, которые указаны в задании, а также для выбранных марок ферромагнитных материалов определяем требуемую магнитодвижущую силу (МДС) F=Iw, а,следовательно, при известном количестве витков катушки w и ее ток I .
На втором этапе решается обратная задача – по известной величине магнитодвижущей силы F определяется величина магнитного потока в магнитопроводеФ, а также величина магнитной индукции B в отсутствии зазора. Затем для нескольких значений воздушного зазора (в диапазоне от 0 до  ) определяются величины магнитной индукции Bd в зазоре для расчета тяговой характеристики электромагнита.
) определяются величины магнитной индукции Bd в зазоре для расчета тяговой характеристики электромагнита.
Учитывая, что по условию задачи потоками рассеивания и полями выпучивания можно пренебречь, то магнитный поток вдоль всей цепи будет одинаковым. Поток в обоих магнитных участках и поток в воздушном зазоре, от которого зависит тяговое усилие, равны ФмА = ФмВ = Фd = Ф .
1. Прямая задача
Алгоритм решения прямой задачи:



 ВА НА НАlмА
ВА НА НАlмА



 Ф ВВ НВ НВlмВ НАlмА +НВlмВ + 2Нd d =
Ф ВВ НВ НВlмВ НАlмА +НВlмВ + 2Нd d =



 Вd Нd Нd d =Iw I
Вd Нd Нd d =Iw I
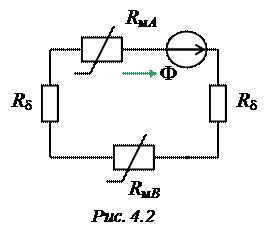
Направление магнитного потока Ф в сердечнике и направление МДС для схемы замещения (рис. 4.1 и 4.2) определяются по правилу правоходового винта в соответствии с направлением тока I в обмотке.
|
 По заданному потокуФи сечениям Sk находят магнитные индукции на каждом участке
По заданному потокуФи сечениям Sk находят магнитные индукции на каждом участке


Величина сечения воздушного зазора Sd принимается равной SВ, так как потоками выпучивания в зазоре, по условию задачи, можно пренебречь
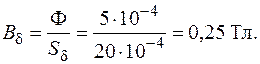
По кривым намагничивания сталей 2213 и 3404 (рис.4.3 и 4.4) определяются напряженности поля Hk для ферромагнитных участков цепи
ВА Þ HА » 111 А/м
ВВ Þ HВ » 15 А/м
Напряженность поля Hd в зазоре
 ,
,
где μо = 4π ×10-7 Гн/м – постоянная, абсолютная магнитная проницаемость вакуума
|
|
|




Рис. 4.3. Сталь2213. Основная кривая намагничивания
|
|




Рис.4.4. Сталь3404. Основная кривая намагничивания
Искомая МДС будет равна сумме падений магнитного напряжения вдоль всей магнитной цепи
F = Iw = HА lМА+HВ lВМ+ 2Hddmax =
= 111 × 0,45 +15× 0,15+ 2×199045× 10 -3 » 450 А
Величина тока I в катушке (число витков w катушки задано):
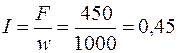 А.
А.
При известных: токе I и магнитном потоке Ф, можно также рассчитать индуктивность катушки L.
Потокосцепление Y можно определить (фактически дословно) как произведение магнитном потока Ф на число витков катушки w с которыми он сцеплен
Y = Ф w и одновременно Y = L I.
Следовательно, индуктивность катушки L составит:
 .
.
Тяговое усилие, возникающее в одном зазоре Fтяг d для исходного состояния электромагнита (при dmax) определяется по формуле (3.6) и составит:
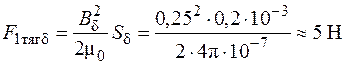 .
.
Так как в магнитной цепи два зазора (рис.4.1), то общее тяговое усилие электромагнита составит:
Fтяг=2 Fтягd =10 Н.
2. Обратная задача
При выполнении второго пункта задачи величина магнитодвижущей силы F в магнитной цепи известна и составляет 450 ампер. Необходимо определить величину магнитного потока в магнитопроводеФ, а также величину магнитной индукции B в отсутствии зазора.
Схема замещения (рис.4.2) в этом случае не содержит магнитных сопротивлений зазоров(Rd= 0) , но так как магнитные сопротивления участков магнитопровода неизвестны, необходимо воспользоваться алгоритмом решения обратной задачи магнитной цепи, используя графоаналитический метод.
1) Необходимо задаться несколькими значениями магнитной индукции в каком-то сечении, например индукцией магнитного поля в зазоре Вδi (или сразу значением магнитного потока Фi в цепи), и для каждого из них решается прямая задача, то есть определяются значения МДС (Fi) необходимые для создания в зазоре такой Вδi . Расчеты сводятся в табл.4.1.
Так как зазор отсутствует(d=0), то равны нулю Rd и Hd. Тогда, в соответствии с законом Ома для магнитной цепи - уравнением (3.5), магнитный поток Ф будет больше, чем в случае с зазором, даже несмотря на нелинейный характер магнитных сопротивлений участков магнитопровода. Следовательно, начальное минимальное значение магнитного потока Фi в цепи можно выбрать равным или даже несколько большим, чем в цепи по п.1 решаемой задачи.
Таблица 4.1
| Фi×10-4 Вб | ВА, Тл | ВВ, Тл | Вd , Тл | НА, А/м | НВ, А/м | Нd, А/м | F=IW, А |
| 1,0 | 0,8 | - | - | ||||
| 1,06 | 0,85 | - | - | ||||
| 1,2 | 0,95 | - | - | ||||
| 1,3 | 1,05 | - | - | ||||
| 1,4 | 1,15 | - | - | ||||
| 1,5 | 1,2 | - | - |
2) По данным таблицы строится зависимость Ф= f (F) и по ней при заданном значении F = 450 A определяется искомый поток Фd=0 (рис.4.4).

Тяговая характеристика электромагнита
Для построения тяговой характеристики электромагнита при токе катушки, рассчитанным по п.1необходимо определить величину магнитного потока в зазореФd, а также величину магнитной индукции Bdдля промежуточных значений зазора 0 < d < dmax.
То есть, снова решаются обратные задачи при известной величине магнитодвижущей силы F =450 А.
Необходимо задаться значениями зазоров, это удобно сделать в долях от максимального зазора:
d1 = 0,25dmax = 2,5×10 -4 м
d2 = 0,5d max, =5×10 -4 м
d3 = 0,75 d max =7,5×10 -4 м
Решаются три обратные задачи, аналогично тому, как определялась величина магнитного потока при отсутствии зазора.
Расчеты сведены в табл.4.2.
Таблица 4.2
| Фi×10-4 Вб | ВА, Тл | ВВ, Тл | Вd, Тл | НА, А/м | НВ, А/м | Нd, А/м | F=IW, А |
| d1 = 0,25d max = 2,5×10 -4 м | |||||||
| 0,8 | 0,8 | 436,06 | |||||
| 1,06 | 0,85 | 0,85 | |||||
| 1,2 | 0,95 | 0,95 | |||||
| 1,3 | 1,05 | 1,05 | |||||
| 1,5 | 1,2 | 1,2 | |||||
| d1 = 0, 5d max = 5×10 -4 м | |||||||
| 0,44 | 0,35 | 0,35 | |||||
| 0,81 | 0,65 | 0,65 | |||||
| 0,8 | 0,8 | ||||||
| 1,06 | 0,85 | 0,85 | |||||
| 1,2 | 0,95 | 0,95 | |||||
| 1,3 | 1,05 | 1,05 | |||||
| 1,5 | 1,2 | 1,2 | |||||
| d1 = 0, 75d max = 7,5×10 -4 м | |||||||
| 0,25 | 0,2 | 0,2 | |||||
| 0,8 | 0,8 | ||||||
| 1,06 | 0,85 | 0,85 | |||||
| 1,2 | 0,95 | 0,95 | |||||
| 1,3 | 1,05 | 1,05 | |||||
| 1,5 | 1,2 | 1,2 |
По данным табл.4.2 строятся зависимости Фdi= f (F), и по ним определяются искомые потоки Фdi ( рис.4.5).

Фd1 »16,5×104Вб
Фd2 »9,2×104Вб
Фd3 »7,1×104Вб
Далее рассчитываем значения Вdi (не забудем и значение Фd=0)
Вd=0 =23,2×10 -4/20×10-4=1,16 Тл,
В(d=2,5×10 –4) =16,5×10 -4/20×10-4=0,825 Тл,
В(d= 5×10 –4) =9,2×10 -4/20×10-4=0,46 Тл,
В(d= 7,5×10 –4) =7,1×10 -4/20×10-4=0,355 Тл,
а также тяговое усилие электромагнита для величин зазоровd i по выражению:
Fтяг i =2 Fтяг d =Вd 2× Sd / μо
Fтяг d=0 = 2142 Н
Fтяг (d=2,5×10 –4) = 1083 Н
Fтяг (d= 5×10 –4) = 337 Н
Fтяг (d= 7,5×10 –4) = 201 Н
Построим тяговую характеристику электромагнита FТяги=f(d) (рис. 2.4.6) с учетом точки, рассчитанной для исходного состояния зазора dMAX (Fтяг dмах =1990 Н).
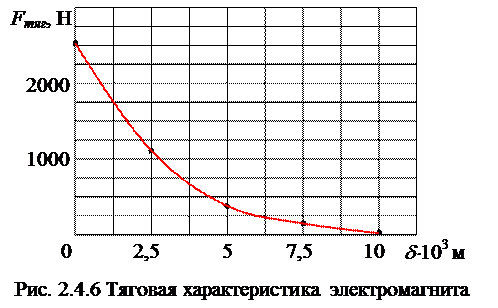
 Материал: Сталь 2213-уч.А
Сталь 3404-уч.В
Материал: Сталь 2213-уч.А
Сталь 3404-уч.В
