Відцентрові насоси

Визначення напірної характеристики насосу

Насосом називається гідравлічна машина, яка призначена для пе­реміщення рідини шляхом передачі їй механічної енергії. Насос, одержуючи механічну енергію від якогось джерела, передає її пото­кові рідини, що рухається. Основними параметрами насосів є напір (або тиск), подача, потужність і коефіцієнт корисної дії.

Напір являє собою збільшення питомої енергії рідини на ділянці від входу насосу до виходу з нього. Напір, утворюваний насосом, вимірюється в метрах стовпа перекачуваної рідини, що еквівалентно підйому рідини на визначену висоту h.

Подача – це об’єм рідини, який подається до трубопроводу за оди­ницю часу і зазвичай вимірюється в кубічних метрах за секунду (м³/с), кубічних метрах за годину (м³/год), літрів за хвилину (л/хвил).

Потужність характеризується витратою насосом енергії на переміщення рідини.

Коефіцієнт корисної дії враховує всі види втрат, пов'язані з перетворенням механічної енергії двигуна в енергію потоку рідини, що рухається. Як джерело механічної енергії для приводу на­сосів частіше за все використовують електродвигуни, рідше – дви­гуни внутрішнього згоряння. Існує багато насосів, які різняться між собою за принципом дії, конструкцією та потужністю. За принципом дії насосі розподіляють на динамічні та об'ємні.

У насосах динамічного принципу дії передача енергії відбу­вається в камері постійного об’єму, що з'єднується з вхідним і вихідним патрубком насоса. В свою чергу вони розподіляються на лопатні насоси й насоси тертя. Об'ємні насоси забезпечують пере­качування рідини робочою камерою, яка періодично змінює свій об'єм за рахунок обертального або зворотно-поступального руху робочого ор­гану.

Найбільш поширені на складах ПММ насоси відцентрові, вихрові, поршневі, шестеренні та ґвинтові.

Відцентрові насоси

Найбільш поширеним насосом на складах ПММ є відцентрові насо­си. Вони характеризуються простотою конструкції та високою надійністю в ро­боті. Насоси добре компануються з електродвигу–нами в один агрегат.

Відцентрові насоси мають великий діапазон подач (від декількох кубічних сантиметрів за хвилину (см³/хв) до 200 – 400 кубічних метрів за годину (м³/год). Напір відцентрових насосів може досягати значення 150 – 200 м. Коефіцієнт корисної дії значних відцентро­вих насосів лежить у межах 0,9–0,92, а для насосів із малою подачею в межах 0,6–0,75.

Насоси у залежно від напору, створюваного ними, розрізняють на високонапірні (напір більш 60 м, средньонапірні – 20–60 м) і низьконапірні (напір менше 20 м).

Відцентровий насос, як правило складається з корпуса 2

(рис. 4.1) із патрубками входу 1, виходу 4 і робочого колеса 3, яке закріплено на валу. Між корпусом і валом встановлене ущільнення.

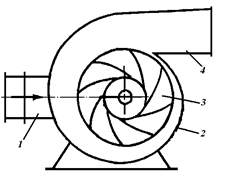
Рис. 4.1. Схема відцентрового насоса: 1– вхідний патрубок; 2– корпус; 3– робоче колесо; 4– патрубок виходу рідини.

 

При обертанні робочого колеса з деякою кутовою швидкістю  на окремий елементарний об’єм рідини в міжлопатній частині робочого колеса буде діяти відцентрова сила

F=m w²r,

де m– маса об’єму рідини; r – радіус обертання елементарного об’єму рідини.

Під дією цієї сили рідина почне переміщуватися до периферії робо­чого колеса і потім проникає у вихідний патрубок. Внаслідок нерозривності рідини, міжлопатний проміжок буде заповнюватися рідиною, що над­ходить до центру робочого колеса через вхідний патрубок 2.

Тиск, який створює насос, можна визначити, уклавши рівняння балансу енергії на вході і виході насоса. Відповідно до рівняння Бернуллі енергія на вході в насос може бути визначена фурмулою:

p₁v₁²
E₁ = z₁ + --- + ---- ,

r 2g

де E₁– енергія потоку рідини на вході до насосу; z₁– висота центру перетину вхідного патрубка, м; p₁– тиск на вході до насосу, кг/м²;

v₁ – швидкість руху рідини у вхідному патрубку, м/с  – густина рідини, кг/м³.

Аналогічне рівняння можна скласти і для вихідного перетину на­соса:

p₂ v₂²

E₂ = z₂ + --- + --- .
r2g

Збільшення енергії перекачуваної рідини визначається як різниця енергії рідини на вході і виході з насоса:

p₂– p₁v₂²–v₁²

E₂ – E₁ = z₂ – z₁+ –––––– +–––––––.
r 2g

Для спрощення виразу можна припустити, що z₁=z₂ а v₁=v₂. Тоді

p₂– p₁
E₂ – E₁= ----- ,

r
враховуючи, що p = h r:

Для спрощення виразу можна припустити, що z₁=z₂ а v₁=v₂. Тоді

p₂– p₁
E₂ – E₁= ----- ,

r
враховуючи, що p = h r:

E₂ – E₁ = h₂ – h₁= H.

Таким чином, збільшення енергії потоку рідини визначається збільшенням напору на значення у h. Потужність, яка витрачається на переміщення рідини, називається корисною потужністю N_к:

Vr H

N_к= ---- ,
t

де V – об’ємрідини, перекачиваємої насосом запевний час. З огляду на те, що V/t = Q, отримаємо

N_к = Q r H

Енергія, спожита насосом, буде більше корисної потужності за рахунок різноманітного роду втрат. Ці втрати враховуються ко­ефіцієнтом корисної дії h, що являє собою відношення корис­ної потужності N_кдо потужності, спожитої насосом N.

N_к

h= ----.

N

Втрати енергії в насосі можна представити сумою трьох основних видів втрат: гідравлічних, механічних і об'ємних:

h = h_г^. h_м^. h_об,

де h_г– гідравлічний ККД; h_м – механічний ККД; h_об– об'ємний ККД. Для більшості відцентрових насосів h_г =0,8 – 0,96, h_м= 0,9–0,97, h_об=0,95–0,98.

Гідравлічні втрати енергії в насосі складаються з втрат на тертя рідини о різноманітні внутрішні поверхні насоса й утворення вихрових течій, пов'язаних із численними поворотами вектора швидкості потоку в насосі, різкими розширеннями, а також звужен­нями внутрішніх каналів.

Об'ємний ККД (h_об) враховує внутрішнє перетікання рідини че­рез зазори між обертовим робочим колесом і нерухомими деталями корпуса з області високого тиску в околиці низького тиску. Якщо вказані витоки рідини позначити через витрату DQ, то об'ємний ККД насоса можна визначити виразом

Q

h_об= ----- ,

Q+ DQ

де Q – витрата рідини у напірному трубопроводі.

Механічні втрати пов'язані з витратою енергії на тертя вала в підшипниках і ущільненнях, а також тертя робочого колеса о рідину. Загальний ККД сучасних відцентрових насосів дорівнює 0,9 – 0,92 для великих насосів і 0,6 – 0,75 – для насосів малої потужності.

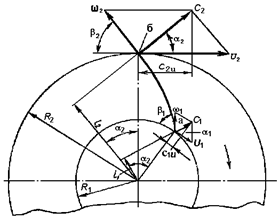
Напір, який утворює насос, і його ККД тісно пов'язані значенням та напрямком швидкостей потоку перекачуємої рідини в міжлопатних каналах робочого колеса (рис. 4.2).

.

 

Рис. 4.2. План швидкостей потоку рідини в міжлопаточних каналах відцентрового насоса.

Q

C_r (4.1)

2  r b

Відносна швидкість спрямована по дотичній до поверхні ло­патки. Радіальну складової абсолютної швидкості можна визначити за умови що потік нерозривний. Уся перекачувана рідина проходить через кільцевий перетин робочого колеса радіусом r і шириною b за винятком площі, що займає тіло лопаток. Цю площу можна обчислити, ввівши коефіцієнт
стиснення перетину тілом лопаток 

Знаючи значення і напрямок окружної швидкості u і радіальну складову абсолютної швидкості C_r, можна визначити значення і нап­рямок відносної швидкості W. Для цього необхідно побудувати пара­лелограм швидкостей: із кінця вектора C_r провести пряму паралель­но напрямку вектора швидкості u до перетинання з напрямком віднос­ної швидкості W, потім із кінця вектора u пряму, паралельно векто­ру W. Діагональ отриманого паралелограма і буде вектором абсолютної швидкості С_r потокові рідини в міжлопатних каналах робочого ко­леса. Аналітичне вираження значення цих швидкостей можна одержати, якщо відомі кути  і  між отриманими векторами швидкостей:

Q

C_r = ------ . (4.1)

2 p r b y

Відносна швидкість спрямована по дотичній до поверхні ло­патки. Радіальну складової абсолютної швидкості можна визначити за умови що потік нерозривний. Уся перекачувана рідина проходить через кільцевий перетин робочого колеса радіусом r і шириною b за винятком площі, що займає тіло лопаток. Цю площу можна обчислити, ввівши коефіцієнт
стиснення перетину тілом лопаток y.

Знаючи значення і напрямок окружної швидкості u і радіальну складову абсолютної швидкості C_r, можна визначити значення і нап­рямок відносної швидкості W. Для цього необхідно побудувати пара­лелограм швидкостей: із кінця вектора C_r провести пряму паралель­но напрямку вектора швидкості u до перетинання з напрямком віднос­ної швидкості W, потім із кінця вектора u пряму, паралельно векто­ру W. Діагональ отриманого паралелограма і буде вектором абсолютної швидкості С_r потокові рідини в міжлопатних каналах робочого ко­леса. Аналітичне вираження значення цих швидкостей можна одержати, якщо відомі кути a і b між отриманими векторами швидкостей:

Q

W = C_r/sin b= --------- ;

2p b r y sin b

Q

C = C_r/sin a = ---------- ,

2p b r y sin a

де y = ( t–s)/t – коефіцієнт стиснення потоку; t = 2pr/z – крок розташування лопатей на околі радіусом r; s – товщина лопаті. Складаний характер руху потоку рідини в міжлопатній частині насоса призводить до того, що при створенні нових високо­потужних насосів доводиться паралельно займатися і розрахунково-теоретичною розробкою конструкції їхньої проточної частини, і прове­денням експериментів, а також використовувати дані, отримані в процесі експлуатації аналогічних насосів.

Теоретичний напір, утворюваний насосом, визначається рівнянням Єйлера:

 

H_т = (u²C₂cos a₂ – u₁C₁cosa₁)/g

З цього рівняння зрозуміло, що найбільший теоретичний тиск ут­ворюється при a₁ = 90⁰, тобто коли cos a₁ = 0⁰. Тому кривизна лопаток на вході до колеса береться такою, щоб a₁= 90⁰, тоді

H_т= u₂C₂cos a₂/g (4.2)

У сучасних насосах кут a₂= 8⁰.. 15⁰ (іноді a₂= 20⁰) вибирається з умови найвищого ККД насоса, а кут b₁ = 15⁰ - 25⁰, що створює умови для безударного входу рідини на лопатку робочого колеса. Швидкість C₁ може мати значення 2 – 4 м/с, при частоті обертання робочого колеса 960 – 2950 об/хв.

Тиск, утворюваний насосом, відрізняється від теоретичного на значення у гідравлічних втрат енергії всередині насосу.

У відцентрових насосах можуть застосовуватися лопатки трьох типів за кривизною щодо напрямку обертів робочого колеса:

загнуті назад (рис. 4.3а);

ті, що закінчуються радіально (рис. 4.3б );

 

Рис. 4.3. Форми лопаток робочих коліс

Для з'ясовування впливу кривизни лопаток на значення теоретич­ного напору роздивимося паралелограм швидкостей на

рис. 4.2.

U₂ = C₂ cos a₂+ Cr₂ ctg b₂,

тоді

С₂ cos a₂ = U₂ – Cr₂ctg b₂ ,

де Cr₂ – радіальна складової абсолютної швидкості рідини на ви­ході з міжлопатної частини колеса.

Підставляючи цей вираз в рівність (4.2), отримаємо

 

 

H_т = U₂ (U₂ – Cr₂ctg b₂)/g (4.3)

Застосовуючи цей вираз до лопаток різних форм, одержи­мо:

для лопаток, загнутих назад:

b₂< 90^о, ctg b₂> 0 ;

для ло­паток, що радіально закінчуються:

b₂ <90о, ctg b2 = 0;

для ло­паток, загнутих уперед:

b₂> 90^о, ctg b₂< 0.

Робочі колеса, в яких лопатки відігнуті вперед, створюють найбільший теоретичний тиск за рахунок більш високої швидкості на виході з колеса. Проте велика швидкість призводить і до підвищення опору, що суттєво позначається на дійсному тиску, який створює насос.

Залежність тиску, утворюваного насосом від прокачування, нази­вається характеристикою насоса. Теоретичну характеристику H = f(Q) можна визначити аналітично.

Підставивши вираз (4.1) у рівняння (4.3), одержимо формулу для теоретичного напору, де буде показана його залежність від витрати:

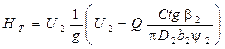(4.4)

Цей вираз можна записати і в такому вигляді:

H_т = A–B ,

U₂ctg b₂
де A=U₂²/g , а B = --------- ,

pD₂b₂y₂g

 

де U₂, b₂, D₂, b₂, y₂ є постійними для цього насоса, при нез­мінній частоті обертання робочого колеса.

Отримане вираження являє собою рівняння прямої лінії, яка називається теоретичною характеристикою насоса.

На рис. 4.4 показані теоретичні характеристики насосів, що ма­ють різні види лопаток.

 

З формули (4.4) випливає що:

при Q=0 H_т = U₂²/g зі збільшенням прокачування в робочому колесі з лопатками відігнутими вперед ctg b₂< 0 теоретичний тиск зростає;

для робочого колеса з радіальними лопатками ctgb₂ = 0 теоре­тичний тиск залишається постійним і визначається формулою H_т = U₂²/ g;

для відігнутих назад лопаток ctgb₂>0 і теоретичний напір, утворюваний робочим колесом, із збільшенням прокачування падає.

Рис. 4.4. Характеристики насосів с різними формами робочих коліс

1– робоче колесо з лопатами, відігнутими назад; 2– робоче колесо з радіальними лопатками; 3– робоче колесо з лопатками, відігнутими вперед.

 

Найбільший теоретичний напір, утворюваний насосом, у робочому колесі з лопатками, загнутими вперед. Дійсний напір, утворюваний насосом, одержують експериментально, при цьому визначають корисну і затрачену потужність, розраховують коефіцієнт корисної дії насосу і визначають оптимальний режим роботи, тобто Q і H при максима­льному ККД.

Подача, тиск і спожита потужність при роботі насоса залежать від частоти обертання робочого колеса і характеризуються такими спів­відношеннями:

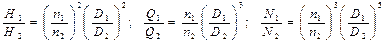(4.5)

Ці співвідношення називають формулами геометричної і кінемати­чної подоби відцентрових насосів і справедливі, якщо частота обертання і діаметр робочого колеса не змінюються більш, ніж на 20 %.

Відцентрові насоси розподіляють на тихохідні, нормальні та швидкохідні. Критерієм оцінки може бути так званий коефіцієнт швидкохідності (n_s), що погоджує між собою такі основні параметри насоса, як подачу Q, напір і частоту обертання n.

Під коефіцієнтом швидкохідності розуміють частоту обертання n_s насоса, який при роботі створює на виході напір H_s, що дорівнює одному метру, і роз­виває корисну потужність N=0,736 кВт (тобто 1 к.с.), що відповідає подачі Q_s = 0,075 м³/с при найбільшому значенні ККД насоса. Значення коефіцієнта швидкохідності можна одержати, вико­ристовуючи рівняння для однотипних насосів із робочими колесами різноманітних діаметрів D, що працюють із різноманітною частотою обертання. Для цієї мети використовуємо формули (4.5):

.

Виключимо з цих виразів D. Для цього перше рівняння возведемо у квадрат, друге в куб і потім поділимо рівняння одне на одне:

 

.

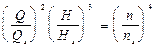Тоді
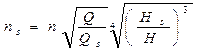. (4.6)

Підставимо в рівняння (4.6) значення H_s = 1 м, Q_s= 0,075 м³ , і отримаємо:

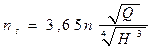. (4.7)
Аналіз формули (4.7) показує, що зі збільшенням напору ко­ефіцієнт швидкохідності насоса зменшується, збільшення ж подачі,

навпаки, збільшує значення коефіцієнта n_s. Залежно від зна­чення коефіцієнта швидкохідності насоси поділяються на ти­хохідні (n_s = 150–300), нормальні (n_s=80–150) і швидкохідні (n_s=150–300). Тихохідні відцентрові насоси мають найбільше відношення діаметрів D₂/D₀ (табл. 4.1), тому забезпечують малу подачу, але розвивають великий напір.

Таблиця 4.1

Класифікація насосів за значенням і коефіцієнта швидкохідності

 

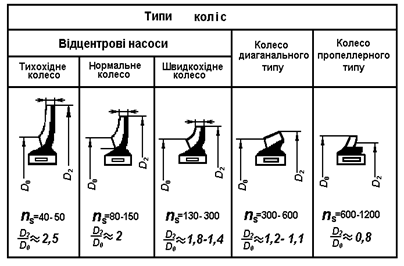
Колеса великої швидко­хідності забезпечують великі подачі та створюють малі напори. Для визначення коефіцієнта швидкохід–ності багатоступеневого насоса у формулу (4.7) слід підставити значення напору, що припадає на одне робоче колесо.

Для насосів з двостороннім підведенням рідини у формулу (4.7) замість Q підставляють Q/2.