П.1 Средние характеристики выборки

Числовые характеристики выборки

 

 

По результатам выборочных наблюдений вычисляются такие статистические выборочные характеристики, как выборочные средняя, дисперсия, среднее квадратичное отклонение, коэффициент корреляции и т.д. Эти характеристики определяют соответствующие параметры генеральной совокупности. Выборочные характеристики представляют собой случайные величины, зависящие от самой выборки.

 

п.1 Средние характеристики выборки

Пусть x₁, x₂, …, x_n – выборка из генеральной совокупности объёма n.

Выборочной средней (или средним значение выборки) называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂, …, x_n признака выборки объема n различны, то

. (1)

Если все значения признака x₁, x₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k , причем n₁+n₂+ …+n_k= n, то

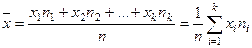. (2)

Если дано распределение непрерывной случайной величины, то вместо x_i, берут середину интервала, т.е. .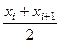

Выборочной дисперсией называется среднее арифметическое квадратов отклонения наблюдаемых значений выборки от их среднего значения .

Если все значения x₁, x₂, …, x_n признака выборки объема n различны, то

. (3)

Если все значения признака x₁, x₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k , причем n₁+n₂+ …+n_k= n, то

. (4)

Преобразуем формулу (3):

 

.

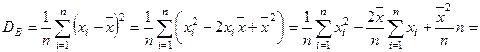
Таким образом, для вычисления выборочной дисперсии можно пользоваться формулой:

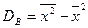. (5)

Выборочная дисперсия имеет систематическую ошибку, приводящую к уменьшению дисперсии. Чтобы это устранить вводят поправку, умножая D_B на . В результате получают исправленную (или модифицированную) дисперсию:

. (6)

Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой – средним квадратичным отклонением.

Выборочным средним квадратичным отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

. (7)

Отметим некоторые важные свойства выборочных среднего и дисперсии в виде теорем.

Теорема 1. Сумма отклонений отдельных значений x_i от их среднего равно нулю:

.

Теорема 2. Пусть X₁, X₂, …, X_n – независимые одинаково распределённые случайные величины, причём , , . Тогда для случайной величины 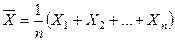имеем:

, .

Следствие. Если X₁, X₂, …, X_n – случайные величины, нормально распределённые по закону , то случайная величина имеет нормальное распределение .

При описании рядов, в которых изучаемое свойство находится в обратно-пропорциональной зависимости от значений влияющего на него фактора, используется средняя гармоническая.

Средней гармонической выборки называется величина обратная средней арифметической из обратных значений вариантов:

. (8)

В некоторых исследованиях требуется определить среднюю величину так, чтобы при замене ею каждого варианта, произведение вариантов оставалось бы неизменным. Для этих целей используется средняя геометрическая.

Средней геометрической называется корень степени, равный числу вариантов, из их произведения:

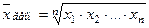. (9)

Средняя геометрическая применяется для характеристики средних темпов изменения какого-либо явления за определённый период.

Отклонение каждого варианта от выборочного среднего характеризуется абсолютной величиной разности , а весь ряд отклонений характеризует вариацию признака в совокупности.

Средним линейным отклонением называется средняя арифметическая абсолютных величин отклонений вариантов от их выборочной средней:

. (10)