Основное уравнение центробежных машин Эйлера

Определим полный напор, развиваемый рабочим колесом при перека-чивании идеальной жидкости. Допустим, что колесо неподвижно, а жидкость движется по каналам между лопатками с той же относительной скоростью, что и во вращающемся колесе. Абсолютные скорости движения жидкости на входе в колесо с₁ и на выходе из колеса с₂ являются каждая геометрической суммой относительной и окружной скоростей, поэтому их можно разложить (рис. 4) на относительные составляющие w₁ и w₂ (направленные вдоль лопаток) и окружные составляющие u₁ и u₂ соответственно (направленные по касательной к окружности вращения).

Рис. 4. К выводу основного уравнения центробежных машин

Принимая за плоскость сравнения плоскость рабочего колеса, составим баланс энергии жидкости при прохождении ее через колесо по уравнению Бер-нулли (z₁ = z₂):

. (17)

При вращении колеса жидкость на выходе приобретает дополнительную энергию А, равную работе центробежной силы на пути длиной r₂ – r₁. Тогда

. (18)

Если рабочее колесо вращается с угловой скоростью w, то центробежная сила С, действующая на частицу жидкости массой т, равна

где G - вес частицы; r - текущий радиус вращение частицы.

После ряда преобразований уравнение (18) запишется в виде

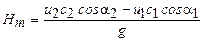. (19)

Уравнение (21) называется основным уравнением центробежных машин и может быть применено к расчету всех центробежных машин, в том числе турбогазодувок, турбокомпрессоров и вентиляторов. Оно верно в том случае, когда все частицы жидкости движутся в насосе по подобным траекториям. Это возможно лишь при условии, что рабочее колесо имеет бесконечно большое число лопаток и сечение канала для прохода жидкости невелико.

Обычно жидкость, поступая из всасывающего трубопровода, движется по колесу в радиальном направлении. В этом случае

. (20)

Уравнение (20) показывает, что напор насоса пропорционален квадрату числа оборотов рабочего колеса (так как ) и зависит от формы лопаток. При этом возможны три случая:

1. Лопатки загнуты в направлении вращения рабочего колеса: > 90°, cos <0 и Н_т> .

2. Лопатки загнуты в направлении, обратном направлению вращения колеса: < 90°, cos >0 и Н_т< .

3. Лопатки не имеют наклона: = 90°, cos = 0 и Н_т= .

Отсюда следует, что теоретически наибольший напор достигается в насосе с лопатками, загнутыми в направлении вращения колеса, наименьший — в противоположном направлении. Несмотря на это насосы изготавливают с небольшими углами ( < 90°) наклона лопастей, так как с возрастанием pg увеличиваются гидравлические потери и уменьшается гидравлический КПД насоса.

Способность рабочего колеса создавать избыточное давление характеризуется степенью реактивности колеса 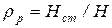, где Н_ст – статический напор, создаваемый колесом. При уменьшении угла скорость с₂ (рис. 4) уменьшается и 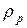возрастает. При этом большая доля напора насоса Н создается в виде давления (потенциальной энергии) в самом колесе насоса.

Действительный напор насоса меньше теоретического, так как часть энергии жидкости расходуется на преодоление гидравлических сопротивлений внутри насоса и жидкость в нем при конечном числе лопаток не движется по подобным траекториям. Действительный напор составляет

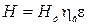где – гидравлический КПД насоса, равный 0,80…0,95; – коэффициент, учитывающий конечное число лопаток в насосе, равный 0,6…0,8.

Значительные потери напора, возникающие в центробежном насосе, обусловливают снижение его общего КПД.

Производительность центробежного насоса Q соответствует расходу жидкости через каналы шириной b₁ и b₂ между лопатками рабочего колеса (рис. 4):

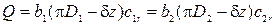, (23)

где d – толщина лопаток; z – число лопаток ; b₁ и b₂ – ширина рабочего колеса на внутренней и внешней окружностях соответственно; 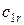и – радиальные составляющие абсолютных скоростей на входе в колесо и выходе из него ( 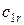= ).