ВВЕДЕНИЕ

 

Явления электронной эмиссии и разряда в газе позволяют получать потоки электронов и ионов, движущихся в вакууме практически без соударений. Электрические и магнитные поля, воздействуя на движущиеся заряженные частицы, изменяют их скорость и траекторию. В электрическом поле напряженности 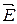на частицу, обладающую зарядом Q, действует сила

, (1)

В магнитном поле на движущуюся заряженную частицу действует сила Лоренца

, (2)

где 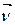– скорость движения частицы; 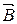– вектор магнитной индукции.

Уравнение движения частицы в пространстве, где имеются и электрическое, и магнитное поля, согласно второму закону Ньютона имеет следующий вид:

, (3)

Это уравнение показывает, что движение заряженной частицы в силовых полях зависит от отношения , которое называется удельным зарядом данной частицы. Следовательно, изучая движение различных заряженных частиц в электрическом и магнитном полях, можно определить удельный заряд частицы и тем самым получить сведения о природе частиц.

Удельный заряд электрона можно определить различными методами. Наиболее распространенными из них являются метод магнитной фокусировки и метод магнетрона.

Метод измерений

Рисунок 1.Лампа

В данной работе для определения удельного заряда электрона используют метод магнетрона.

Магнетрон – это двухэлектродная электронная лампа (диод), в которой управление током осуществляют внешним магнитным полем. Это поле создается соленоидом, внутри которого расположена лампа. Накаливаемый катод и холодный анод лампы имеют форму коаксиальных (соосных) цилиндров (см. рисунок 1).

Линии электрического поля 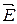внутри магнетрона направлены радиально от анода к катоду, а постоянное магнитное поле 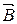направлено вдоль оси катода. Таким образом, магнитное и электрическое поля взаимно перпендикулярны. Напряженность поля E максимальна у катода. В случае, если катод имеет форму тонкой нити, величина E, пропорциональная 1/r, быстро уменьшается с ростом расстояния r от катода. Поэтому изменение скорости электронов до значения, равного v, происходит, в основном, вблизи катода, а при дальнейшем движении можно считать скорость практически постоянной.

Электрон, ускоренный разностью потенциалов U, приобрел кинетическую энергию mv²/2=eU

и имеет скорость

, (4)

В отсутствие магнитного поля электроны, эмитированные катодом, движутся под действием электрического поля 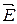прямолинейно в радиальных направлениях. При этом в анодной цепи протекает ток, величина которого зависит от анодного напряжения и тока накала катода. При помещении лампы в магнитное поле B на движущиеся электроны действует сила Лоренца. Она перпендикулярна линиям , т.е. лежит в одной плоскости с вектором скорости электрона 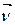, нормальна ему и сообщает частице центростремительное ускорение. Согласно второму закону Ньютона

evB = mv²/R, (5)

 

Таким образом, электрон в магнетроне будет двигаться по окружности, радиус которой

R = mv/eB, (6)

 

уменьшается с ростом индукции магнитного поля. На рисунке 2 показано, как изменяются траектории движения электрона в цилиндрическом магнетроне по мере увеличения магнитной индукции.

Существует критическое значение магнитной индукции B_кр, при котором, как показано на рисунке 2, траектории электронов касаются поверхности анода, а их радиус

R = r/2,

где r – радиус анода.

Согласно соотношениям (4) и (6) значение B_кр зависит от скорости электрона v и соответствующего ей анодного напряжения :

, (7)

Строгий расчет значения B_кр приведен в приложении 2.1.

Если величина B < В_кр, то все электроны достигают анода и анодный ток имеет такое же значение, как и в отсутствие магнитного поля (горизонтальный участок графика на рисунке 2). Если B > В_кр, то электроны не долетают до анода и ток через лампу равен нулю. При B = В_кр ток должен резко снижаться (пунктирная линия на графике рисунк 2), однако наблюдается плавный ход кривой. Это обусловлено рядом причин: неточная коаксиальность катода и анода, краевые эффекты, вылет электронов из катода с различными скоростями и др.

Определив критическое значение индукции магнитного поля B_кр и использовав соотношение (7), можно рассчитать удельный заряд электрона по формуле

 

 

Рисунок 3. Соленоид

 

, (8)

Индукцию B вычисляют по формуле для поля короткого соленоида:

B = m₀IN(cos a₁ – cosa₂)/2l, (9)

где m₀ = 4p×10^–7 Гн/м – магнитная постоянная; I – ток, текущий в обмотке; N – число витков соленоида; l – длина обмотки; a₁ и a₂ – углы, показанные на рисунке 3 при размещении лампы в центре соленоида,

cos a₁= –cos a₂ = ,

где d – диаметр соленоида.

Подставляя значения косинусов в формулу (9), получаем критическую величину магнитной индукции:

, (10)

где I_кр – значение тока в соленоиде, соответствующее критическому значению магнитной индукции B_кр.

С учетом выражения (10) расчетная формула (8) для определения удельного заряда электрона принимает следующий вид:

, (11)

Для определения критического тока I_кр используют экспериментальную зависимость анодного тока от тока в соленоиде: I_а = f(I) (рисунок 4а), которая по виду подобна зависимости I_а = f(B): при критическом токе в соленоиде наблюдается резкое снижение анодного тока I_а.

Крутизну кривой I_а = f(I) показывает отношение приращений анодного тока и тока в соленоиде . При этом максимум кривой (рисунок 4б) соответствует искомому значению I_кр.

 

Рисунок 4. Определение критического тока

Описание установки

Для определения удельного заряда электрона методом магнетрона собирают электрическую цепь, схема которой приведена на рисунке 5, монтажная схема – на рисунке 6.

 

 

 

Рисунок 5. Электрическая схема: 1 – источник постоянного напряжения «+15 В»; 2 – мультиметр для измерения анодного тока (режим A 2 mA, входы COM, mA); 3 – вакуумный диод; 4 – соленоид; 5 – мультиметр для измерения тока соленоида (режим A 200 mA, входы COM, A); 6 –регулируемый источник постоянного напряжения «0...+15 В»; 7 – напряжение накала катода U_н; 8 – миниблок «Магнетрон»

 

Вакуумный диод 3 подключают к источнику постоянного напряжения «+15 В». Анодный ток лампы I_a измеряют цифровым мультиметром 2. Напряжение U_н на нить накала лампы подают от источника постоянного напряжения «-15 В». Диод установлен внутри соленоида так, что ось анода лампы совпадает с осью соленоида. Соленоид 4 создает магнитное поле, индукцию которого регулируют путем изменения тока I в обмотке с помощью кнопок установки напряжения «0…15 В» (поз.14, рисунок 1, стр. 6). Ток в обмотке соленоида измеряют мультиметром 5.

Порядок выполнения работы

Выполнение измерений

1 Соберите электрическую цепь по монтажной схеме, представленной на рисунке 6.

2 Включите кнопкой «Сеть» питание блока генераторов напряжений. Нажмите кнопку «Исходная установка» (поз. 19, см. рисунок 1 на стр. 6).

3 Кнопками установки напряжения «0…15 В» (поз.14, рисунок 1, стр. 6) установите ток 90 мА в обмотке соленоида и измерьте по мультиметру 2 полученные значения анодного тока I_а. Результаты (значения токов I и I_а) запишите в таблицу. Проведите аналогичные измерения увеличивая ток на 2,5 мА до 200мА.

return false">ссылка скрыта

4 Выключите кнопками «Сеть» питание блока генераторов напряжения и блока мультиметров.

Рисунок 6. Монтажная схема: 2, 5, 8 – см. рисунок 5

Таблица

Параметры магнетрона d = 37 мм, l = 36 мм, N = 2800 витков, r = 3 мм, = 15 В
I, мА							…
, мА
, мА
, мА

 

Обработка результатов измерений

1 Найдите изменение (убыль) анодного тока и тока в соленоиде . Вычислите величину . Результаты запишите в таблицу.

2 Постройте на одном листе (на одном поле графика, см рисунок 4) две зависимости I_а=f(I) и .

3 Определите значение критического тока I_кр в обмотке соленоида по положению максимума на графике производной .

4 По формуле (11) вычислите величину удельного заряда электрона .

5 Сравните полученное значение с табличным (согласно справочным данным = 1,7588047×10¹¹ Кл/кг) и оцените относительную погрешность результата измерений по формуле:

,

6 В выводе сделайте анализ использованного метода определения удельного заряда электрона: укажите возможные источники систематических и случайных погрешностей, пути их устранения или снижения.

 

Контрольные вопросы

1 Запишите формулы для сил и , действующих на заряженную частицу в электрическом и магнитном полях.

2 Какие параметры (скорость 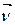, , ускорения , , , радиус кривизны траектории) изменяются при движении заряженной частицы:

а) под некоторым углом к силовой линии электростатического поля,

б) под действием силы Лоренца?

3 Какие уравнения необходимо использовать для определения:

a. а) скорости заряженной частицы, приобретенной в электрическом поле,

b. б) радиуса кривизны траектории электрона в магнитном поле?

4 Покажите на рисунке направление сил и , действующих в магнетроне на электрон, движущийся от катода к аноду.

5 Как и почему изменяются при этом движении модули сил и ?

6 От чего зависят вектор и модуль скорости движения электрона в магнетроне?

7 Покажите на рисунке направление векторов и в магнетроне.

8 От чего зависят форма траектории электрона в магнетроне и значение критической индукции B_кр?

9 Покажите на рисунке форму траектории электрона в магнетроне при различных значениях магнитной индукции (B < B_кр; B = B_кр; B > B_кр).

10 Укажите назначение в электрической цепи мультиметров.

11 От каких величин зависит значение анодного тока магнетрона?

12 Как зависит величина анодного тока магнетрона:

a. а) от тока накала катода ; б) от анодного напряжения ;

b. в) от тока в обмотке соленоиотров: