ВЕРОЯТНОСТИ ГИПОТЕЗ. ФОРМУЛЫ БАЙЕСА
Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) B1, B2, ..., Bn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса:
РА(Вi) = 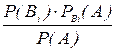 (i = 1, 2, . . . , n),
(i = 1, 2, . . . , n),
где Р(А) = Р(В1)×РB1(А)+Р(В2)×РB2(А ) + ... +Р(Вn)×РBn(А).
Пример 15. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму - 0,4. Вероятность того, что деталь будет признана стандартной первым контролером, равна 0,94, а вторым - 0,98. Деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
Решение. Обозначим через А событие, состоящее в том, что деталь признана стандартной. Можно сделать два предположения:
1) деталь проверил первый контролер (гипотеза В1);
2) деталь проверил второй контролер (гипотеза B2).
Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса
РА(В1) =  .
.
По условию задачи имеем:
P(B1) = 0,6 (вероятность того, что деталь попадет к первому контролеру);
Р(В2) = 0, 4 (вероятность того, что деталь попадет ко второму контролеру);
РВ1(А) = 0,94 (вероятность того, что деталь будет признана первым контролером стандартной);
РВ2(А) = 0,98 (вероятность того, что деталь будет признана вторым контролером стандартной).
Искомая вероятность:
РА(В1) = 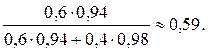
Пример 16. Два стрелка независимо друг от друга стреляют по мишени, делая по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго - 0,4. После стрельбы в мишени обнаружена пробоина. Найти вероятность того, что она принадлежит первому стрелку.
Решение. Обозначим события:
А - в мишени одна пробоина (одно попадание);
А1 - первый стрелок попал в мишень P(А1) =0,8;
А2 - второй стрелок попал в мишень P(А2) =0,4;
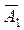 - первый стрелок промахнулся
- первый стрелок промахнулся 
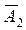 - второй стрелок промахнулся
- второй стрелок промахнулся 
Можно выдвинуть четыре гипотезы:
B1 - только первый стрелок попал в мишень, второй - промахнулся:
Р(В1 ) = Р(А1 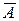 2)=Р(А1)×Р(
2)=Р(А1)×Р( 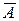 2)=0,8×0,6=0,48,
2)=0,8×0,6=0,48,
B2 - первый стрелок промахнулся, только второй стрелок попал в мишень:
Р(В2) = Р( 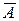 1А2)=Р(
1А2)=Р( 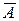 1)×Р(А2)=0,2×0,4=0,08;
1)×Р(А2)=0,2×0,4=0,08;
В3 - оба стрелка не попали в мишень:
Р(В2)= Р(  )=Р(
)=Р( 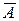 1)×Р(
1)×Р(  )=0,2×0,6=0,12;
)=0,2×0,6=0,12;
B4 - оба стрелка попали в мишень:
Р(В2) = Р(А1А2)=Р(А1)×Р(А2)=0,8×0,4=0,32.
Найдем условные вероятности события А:
РВ1(А) = 1 (вероятность того, что одна пробоина сделана первым стрелком);
РВ2(А) = 1 (вероятность того, что одна пробоина сделана вторым стрелком);
РВ3(А)=0 (вероятность того, что в мишени одна пробоина, если оба попали);
РВ2(А)=0 (вероятность того, что одна пробоина, если оба промахнулись).
Искомую вероятность того, что попал первый стрелок, найдем по формуле Бейеса
