Энтропия. Физический смысл энтропии. Энтропия и вероятность
Энтропия. Физический смысл энтропии. Энтропия при обратимых и необратимых процессах в замкнутой системе. Второе начало термодинамики и превращение теплоты в работу.
Энтропия. Физический смысл энтропии. Энтропия и вероятность
Рассматривая КПД тепловой машины, работающей по циклу Карно,  , можно отметить, что отношение температуры холодильника к температуре нагревателя равно отношению величины количества теплоты, отданного рабочим телом холодильнику, к величине количества теплоты, принятого от нагревателя. Это значит, что для идеальной тепловой машины, работающей по циклу Карно, выполняется и такое соотношение:
, можно отметить, что отношение температуры холодильника к температуре нагревателя равно отношению величины количества теплоты, отданного рабочим телом холодильнику, к величине количества теплоты, принятого от нагревателя. Это значит, что для идеальной тепловой машины, работающей по циклу Карно, выполняется и такое соотношение:  . Отношение
. Отношение 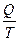 Лоренц назвал приведённой теплотой [1-3,5]. Для элементарного процесса приведённая теплота будет равна
Лоренц назвал приведённой теплотой [1-3,5]. Для элементарного процесса приведённая теплота будет равна  . Значит, при реализации цикла Карно (а он является обратимым циклическим процессом) приведённая теплота остаётся неизменной и ведёт себя как функция состояния, тогда, как известно, что количество теплоты является функцией процесса.
. Значит, при реализации цикла Карно (а он является обратимым циклическим процессом) приведённая теплота остаётся неизменной и ведёт себя как функция состояния, тогда, как известно, что количество теплоты является функцией процесса.
Используя первое начало термодинамики для обратимых процессов,  и деля обе части этого равенства на температуру, получим:
и деля обе части этого равенства на температуру, получим:
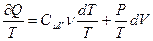 (3.70)
(3.70)
Выразим из уравнения Менделеева - Клапейрона  , подставим в уравнение (3.70) и получим:
, подставим в уравнение (3.70) и получим:
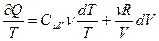 (3.71)
(3.71)
Учтём, что 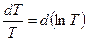 , а
, а  , подставим их в уравнение (3.71) и получим:
, подставим их в уравнение (3.71) и получим:
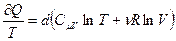 (3.72)
(3.72)
Правая часть этого равенства является полным дифференциалом, следовательно, при обратимых процессах и приведённая теплота тоже является полным дифференциалом, что является признаком функции состояния.
Функция состояния, дифференциалом которой является  , называется энтропией и обозначается S. Таким образом, энтропия – функция состояния. После введения энтропии формула (3.72) будет иметь вид:
, называется энтропией и обозначается S. Таким образом, энтропия – функция состояния. После введения энтропии формула (3.72) будет иметь вид:
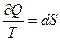 , (3.73)
, (3.73)
где dS – приращение энтропии. Равенство (3.73) справедливо только для обратимых процессов и удобно для расчёта изменения энтропии при конечных процессах:
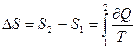 (3.74)
(3.74)
Если система обратимым путём совершает круговой процесс (цикл), то  , а, следовательно, DS=0 , то S = const.
, а, следовательно, DS=0 , то S = const.
Выражая количество теплоты через приращение энтропии для элементарного процесса, и подставляя его в уравнение для первого начала термодинамики, получим новый вид записи этого уравнения, которое принято называть основным термодинамическим тождеством [1-5]:
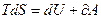 (3.75)
(3.75)
Таким образом, для расчёта изменения энтропии при обратимых процессах удобно использовать приведённую теплоту.
В случае необратимых неравновесных процессов 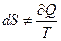 , а для необратимых круговых процессов выполняется неравенство Клаузиуса (доказательство см. в [1,2]):
, а для необратимых круговых процессов выполняется неравенство Клаузиуса (доказательство см. в [1,2]):
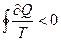 (3.76)
(3.76)
Рассмотрим, что происходит с энтропией в изолированной термодинамической системе. В изолированной термодинамической системе при любом обратимом изменении состояния её энтропия не изменится. Математически это можно записать так: S=0 или S = const.
 Рассмотрим, что происходит с энтропией термодинамической системы при необратимом процессе. Предположим, что переход из состояния 1 в состояние 2 по пути L1 обратим, а из состояния 2 в состояние 1 по пути L2 – необратим (рис.3.13).
Рассмотрим, что происходит с энтропией термодинамической системы при необратимом процессе. Предположим, что переход из состояния 1 в состояние 2 по пути L1 обратим, а из состояния 2 в состояние 1 по пути L2 – необратим (рис.3.13).
Тогда справедливо неравенство Клаузиуса (3.76). Запишем выражение для правой части этого неравенства, соответствующее нашему примеру:
 .
.
Первое слагаемое в этой формуле может быть заменено изменением энтропии, так как этот процесс обратимый. Тогда неравенство Клаузиуса можно записать в виде:
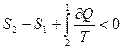 .
.
Отсюда 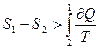 . Так как
. Так как  , то окончательно можно записать:
, то окончательно можно записать:
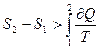 (3.77)
(3.77)
Если система изолирована, то 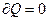 , а неравенство (3.77) будет иметь вид:
, а неравенство (3.77) будет иметь вид:
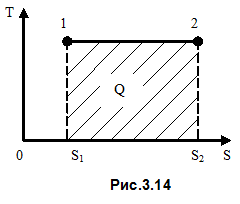
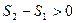 , (3.78)
, (3.78)
то есть энтропия изолированной системы при необратимом процессе возрастает. Рост энтропии продолжается не беспредельно, а до определённого максимального значения, характерного для данного состояния системы. Это максимальное значение энтропии соответствует состоянию термодинамического равновесия. Рост энтропии при необратимых процессах в изолированной системе означает, что энергия, которой обладает система, становится менее доступной для преобразования в механическую работу. В состоянии равновесия, когда энтропия достигает максимального значения, энергия системы не может быть преобразована в механическую работу.
Если же система не изолирована, то энтропия может, как убывать, так и возрастать в зависимости от направления теплообмена.
Энтропия как функция состояния системы, может служить таким же параметром состояния, как температура, давление, объём. Изображая тот или иной процесс на диаграмме (Т,S), можно дать математическую интерпретацию количества теплоты, как площади фигуры под кривой, изображающей процесс. На рис.3.14 приведена диаграмма для изотермического процесса в координатах энтропия – температура.
Энтропия может быть выражена через параметры состояния газа – температуру, давление, объём. Для этого из основного термодинамического тождества (3.75) выразим приращение энтропии:
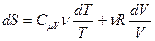 .
.
Проинтегрируем это выражение и получим:
 (3.79)
(3.79)
Изменение энтропии можно выразить и через другую пару параметров состояния – давление и объём. Для этого нужно выразить температуры начального и конечного состояний из уравнения состояния идеального газа через давление и объём и подставить в (3.79):
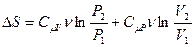 (3.80)
(3.80)
При изотермическом расширении газа в пустоту Т1=Т2, а значит первое слагаемое в формуле (3.79) обнулится и изменение энтропии будет определяться только вторым слагаемым:
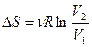 (3.81)
(3.81)
Несмотря на то, что во многих случаях для расчёта изменения энтропии удобно использовать приведённую теплоту, ясно, что приведённая теплота и энтропия – разные, не тождественные понятия.
Рассмотрим физический смысл энтропии. Для этого используем формулу (3.81), для изотермического процесса, при котором не изменяется внутренняя энергия, а всевозможные изменения характеристик обусловлены лишь изменением объёма. Рассмотрим связь объёма, занимаемого газом в равновесном состоянии, с числом пространственных микросостояний частиц газа. Число микросостояний частиц газа, с помощью которых реализуется данное макросостояние газа как термодинамической системы, можно подсчитать следующим образом. Разобьём весь объём на элементарные кубические ячейки со стороной d~10 –10 м (порядка величины эффективного диаметра молекулы). Объём такой ячейки будет равен d3 . В первом состоянии газ занимает объём V1, следовательно, число элементарных ячеек, то есть число мест N1, которые могут занимать молекулы в этом состоянии будет равно  . Аналогично для второго состояния с объёмом V2 получим
. Аналогично для второго состояния с объёмом V2 получим 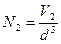 . Следует отметить, что изменение положений молекул соответствует новому микросостоянию. Не всякое изменение микросостояния приведёт к изменению макросостояния. Предположим, молекулы могут занимать N1 мест, тогда обмен местами любых молекул в этих N1 ячейках не приведёт к новому макросостоянию. Однако, переход молекул в другие ячейки, приведёт к изменению макросостояния системы. Число микросостояний газа, соответствующих данному макросостоянию, можно подсчитать, определив число способов размещения частиц этого газа по элементарным ячейкам (основные понятия и формулы элементарной комбинаторики можно посмотреть, например, в [2]). Для упрощения расчётов рассмотрим 1 моль идеального газа. Для 1 моля идеального газа формула (3.81) будет иметь вид:
. Следует отметить, что изменение положений молекул соответствует новому микросостоянию. Не всякое изменение микросостояния приведёт к изменению макросостояния. Предположим, молекулы могут занимать N1 мест, тогда обмен местами любых молекул в этих N1 ячейках не приведёт к новому макросостоянию. Однако, переход молекул в другие ячейки, приведёт к изменению макросостояния системы. Число микросостояний газа, соответствующих данному макросостоянию, можно подсчитать, определив число способов размещения частиц этого газа по элементарным ячейкам (основные понятия и формулы элементарной комбинаторики можно посмотреть, например, в [2]). Для упрощения расчётов рассмотрим 1 моль идеального газа. Для 1 моля идеального газа формула (3.81) будет иметь вид:
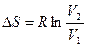 (3.82)
(3.82)
Число микросостояний системы, занимающей объём V1, обозначим через Г1 и определим, подсчитав число размещений NA (число Авогадро) молекул, которые содержатся в 1 моле газа, по N1 ячейкам (местам): 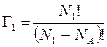 . Аналогично подсчитаем число микросостояний Г2 системы, занимающей объём V2:
. Аналогично подсчитаем число микросостояний Г2 системы, занимающей объём V2:  .
.
Число микросостояний Гi, с помощью которых можно реализовать i- тое макросостояние, называется термодинамической вероятностью данного макросостояния. Термодинамическая вероятность Г ≥ 1.
Найдём отношение Г2/Г1:
 .
.
Для идеальных газов число свободных мест гораздо больше числа молекул, то есть N1 >>NA и N2 >>NA.. Тогда, учитывая выражение чисел N1 и N2 через соответствующие объёмы, получим:

Отсюда можно выразить отношение объёмов через отношение термодинамических вероятностей соответствующих состояний:
 (3.83)
(3.83)
Подставим (3.83) в (3.82) и получим: 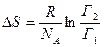 . Учитывая, что отношение молярной газовой постоянной и числа Авогадро, есть постоянная Больцмана k, а также то, что логарифм отношения двух величин равен разности логарифмов этих величин, получим:
. Учитывая, что отношение молярной газовой постоянной и числа Авогадро, есть постоянная Больцмана k, а также то, что логарифм отношения двух величин равен разности логарифмов этих величин, получим:  . Отсюда можно заключить, что энтропия i- того состояния Si определяется логарифмом числа микросостояний, посредством которых реализуется данное макросостояние:
. Отсюда можно заключить, что энтропия i- того состояния Si определяется логарифмом числа микросостояний, посредством которых реализуется данное макросостояние:
 (3.84)
(3.84)
Формула (3.84) называется формулой Больцмана, впервые получившего её и понявшего статистический смысл энтропии, как функции беспорядка. Формула Больцмана имеет более общее значение, чем формула (3.82), то есть может быть использована не только для идеальных газов, и позволяет раскрыть физический смысл энтропии. Чем более упорядочена система, тем меньше число микросостояний, посредством которых осуществляется данное макросостояние, тем меньше энтропия системы. Рост энтропии в изолированной системе, где происходят необратимые процессы, означает движение системы в направлении наиболее вероятного состояния, которым является состояние равновесия. Можно сказать, что энтропия является мерой беспорядка системы; чем больше беспорядка в ней, тем выше энтропия. В этом заключается физический смысл энтропии.
В состоянии термодинамического равновесия молекулы распределены равномерно по объёмам, при этом все направления в пространстве равноправны. В системе наблюдается максимальный беспорядок. Термодинамическая вероятность, а, следовательно, энтропия равновесного состояния системы максимальна.
Неравновесная термодинамическая система после прекращения действия источника, поддерживающего её в неравновесном состоянии, с течением времени переходит в наиболее вероятное равновесное состояние. Такой переход сопровождается ростом энтропии. Следовательно, по изменению энтропии . Отсюда можно заключить, что энтропия i- того состояния Si определяется логарифмом числа микросостояний, посредством которых реализуется данное макросостояние:
 (3.84)
(3.84)
Формула (3.84) называется формулой Больцмана, впервые получившего её и понявшего статистический смысл энтропии, как функции беспорядка. Формула Больцмана имеет более общее значение, чем формула (3.82), то есть может быть использована не только для идеальных газов, и позволяет раскрыть физический смысл энтропии. Чем более упорядочена система, тем меньше число микросостояний, посредством которых осуществляется данное макросостояние, тем меньше энтропия системы. Рост энтропии в изолированной системе, где происходят необратимые процессы, означает движение системы в направлении наиболее вероятного состояния, которым является состояние равновесия. Можно сказать, что энтропия является мерой беспорядка системы; чем больше беспорядка в ней, тем выше энтропия. В этом заключается физический смысл энтропии.
В состоянии термодинамического равновесия молекулы распределены равномерно по объёмам, при этом все направления в пространстве равноправны. В системе наблюдается максимальный беспорядок. Термодинамическая вероятность, а, следовательно, энтропия равновесного состояния системы максимальна.
Неравновесная термодинамическая система после прекращения действия источника, поддерживающего её в неравновесном состоянии, с течением времени переходит в наиболее вероятное равновесное состояние. Такой переход сопровождается ростом энтропии. Следовательно, по изменению энтропии можно судить о направлении протекания самопроизвольного процесса.
Второе начало термодинамики - один из основных законов термодинамики, устанавливающий необратимость макроскопических процессов, протекающих с конечной скоростью. Другими словами, это закон, устанавливающий направление протекания самопроизвольных процессов. Исторически второе начало термодинамики возникло из анализа работы тепловых машин [1-5,10]. Существует несколько формулировок второго начала термодинамики. Во-первых, второе начало термодинамики накладывает ограничения на возможности циклического получения механической работы за счёт полученной теплоты (формулировки Клаузиуса и Томсона (Кельвина)). Во-вторых, второе начало термодинамики с помощью понятия энтропии позволяет судить о направлении протекания процессов в системе (формулировка Больцмана).
Формулировка Клаузиуса.
Теплота не может самопроизвольно перейти от более холодного тела к более нагретому без каких-либо других изменений в системе.