Пример 8.

Какими признаками характеризуется матрица отношения R, если R соответственно: рефлексивно, антирефлексивно, симметрично, антисимметрично, транзитивно?

Ø Пусть R задано на М, R Í М ´ М.

1) R рефлексивно, если для любого а Î М имеет место aRа, т.е. оно выполняется для всех пар (а, а), а Î М. В матрице этим парам соответствуют элементы c_ij. Такие элементы составляют главную диагональ матрицы. Следовательно, главная диагональ матрицы рефлексивного отношения содержит только единицы;

2) R антирефлексивно, если ни для какого а Î М не выполняется aRа. Из этого следует, что главная диагональ матрицы антирефлексивного отношения должна содержать только нули;

3) R симметрично, если для пары (а, b) Î М ´ M из aRb следует bRа, т.е. для любой пары отношение R выполняется в обе стороны либо не выполняется вообще. Таким образом, если в матрице единица стоит на пересечении i-и строки j-го столбца, т.е. с_ij = 1, то она должна стоять и на пересечении j-й строки и i-го столбца, т.е. с_ji = 1, и наоборот, если с_ji = 1, то с_ij = 1. Таким образом, в матрице симметричного отношения с_ij = с_ji, т.е. матрица симметрична относительно главной диагонали;

4) R антисимметрично, если из aRb и bRa следует а=b. Это означает, что в соответствующей матрице ни для каких ij Î [1,2,...m], т = ½М½, i ¹ j, не выполняется с_ij = с_ji = 1. Таким образом, в матрице антисимметричного отношения отсутствуют единицы, симметричные относительно главной диагонали;

5) R транзитивно, если для любых а, b, с из aRb и bRс следует aRс. В матрице такого отношения должно выполняться следующее условие: если в i-й строке стоит единица, например j-й координате (столбце) строки, т.е. с_ij = 1, то всем единицам j-й строке (пусть этим единицам соответствуют k-e координаты такие, что с_jk = 1) должны соответствовать единицы в i-й строке в тех же k-хкоординатах, т.е. c_ik = 1 (и, может быть, еще и в других координатах). Это условие иллюстрируется на рис.6, где кружком выделена единица с_ij= 1, для которой производится проверка условия, а стрелками показана последовательность проверки данного условия.

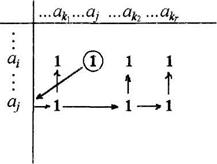
Рис.6

В матрице транзитивного отношения это условие должно выполняться для любых i,jÎ т = ½М½таких, что c_ij=1. И наоборот, если в матрице R имеется хотя бы одна единица с_ij = 1, для которой данное условие не выполняется, то R не транзитивно.