Пример 5.
Составьте матрицы отношений, заданных на системе множествb(М), М={а, b, с}:
1) R - "пересекаться с" (иметь непустое пересечение);
2) 
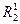- "являться строгим включением Ì".
Ø b(М) = (Æ, {а}, {b}, {с}, {а, b}, (а, с}, {b, с}, {а, b, с}}. Матрицы отношений Rl и R2 представлены на рис.4.
| R1 | Æ | {a} | {b} | {c} | {a,b} | {a,c} | {b,c} | {a,b,c} |
| Æ | ||||||||
| {a} | ||||||||
| {b} | ||||||||
| {c} | ||||||||
| {a,b} | ||||||||
| {a,c} | ||||||||
| {b,c} | ||||||||
| {a,b,c} |
| R2 | Æ | {a} | {b} | {c} | {a,b} | {a,c} | {b,c} | {a,b,c} |
| Æ | ||||||||
| {a} | ||||||||
| {b} | ||||||||
| {c} | ||||||||
| {a,b} | ||||||||
| {a,c} | ||||||||
| {b,c} | ||||||||
| {a,b,c} |
Рис.4
Пример 6.
Для отношений, определенных на множестве М= {а, b, с, d, e, f, g, h} элементов структуры (см. рис.3), составьте матрицы:
1) R1 - "быть частью целого";
2) R2 - "быть непосредственно связанным с".
Ø Матрицы отношений R1 и R2 приведены на рис.5. (При построении матрицы отношения R1 предполагалось, что "целое есть часть самого себя"; аналогично при построении матрицы отношения R2.)
| R1 | a | b | c | d | e | f | g | h |
| a | ||||||||
| b | ||||||||
| c | ||||||||
| d | ||||||||
| e | ||||||||
| f | ||||||||
| g | ||||||||
| h |
| R2 | a | b | c | d | e | f | g | h |
| a | ||||||||
| b | ||||||||
| c | ||||||||
| d | ||||||||
| e | ||||||||
| f | ||||||||
| g | ||||||||
| h |
Рис.5