Пример 1.

R = {(а, b), (а, с), (b, d)}.

2.Матрицей - бинарному отношению R Í М ´ М, где М = {а_1, а₂ ..., а_п}, - соответствует квадратная матрица порядка n, в которой элемент с_ij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если между а и а имеет место отношение R, или 0, если оно отсутствует:

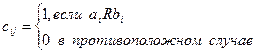
Пример 2.

Пусть М- {1,2,3,4,5,6}. Задайте в явном виде (списком) и матрицей отношение

R Í M ´ M, если R означает "быть строго меньше".

ØОтношение R как множество содержит все пары элементов a, b из М такие, что а < b:

R = {(a,b): a,bÎM; a<b}. Тогда:

R = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}.

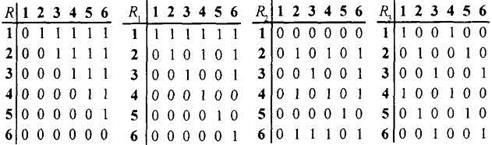
a) б) в) г)

Рис.2