Бинарные отношения. Основные определения.

Лекция 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

 

БИНАРНЫЕ ОТНОШЕНИЯ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

 

1. Отношения.

2. Бинарные отношения. Основные определения.

3. Свойства бинарных отношений.

4. Эквивалентность и порядок.

Отношения

Отношения - один из способов задания взаимосвязей между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые унарные и бинарные отношения.

Унарные (одноместные) отношения отражают наличие какого-то определенного признака R (свойства и т.п.) у элементов множества М (например, "быть белым" на множестве шаров в урне). Тогда все такие элементы а из множества М, которые отличаются данным признаком R, образуют некоторое подмножество в М, называемое унарным отношением R, т.е. а Î R и R Í М.

Бинарные (двухместные) отношения используются для определения каких-то взаимосвязей, которыми характеризуются пары элементов в множестве М (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: "жить в одном городе", "быть моложе", "быть сыном", "работать в одной организации" и т.п.). Тогда все пары (а, b) элементов из М, между которыми имеет место данное отношение R, образуют подмножество пар из множества всех возможных пар элементов М´М= М², называемое бинарным отношением R, т.е. (a, b) Î R, при этом R Í М ´ М.

В общем случае могут рассматриваться п-местные отношения, например отношения между тройками элементов - трехместные (тернарные) отношения и т.д.

Под п-местным отношением понимают подмножество R прямого произведения п множеств: R Í М₁ ´ М₂ ´ ... ´ М_п. Говорят, что элементы а₁, а₂, … a_п (a₁ Î М₁, a₂ Î М₂, … a_n Î М_n) находятся в отношении R, если (а_1, а₂ ..., а_п) Î R. Если n-местное отношение R задано на множестве М своих элементов, т.е. М₁ = М₂ = ... = М_n, то R Í М_n.

Бинарные отношения. Основные определения.

Двухместным, или бинарным, отношением R называется подмножество пар (а, b) Î R прямого произведения М₁ ´ М₂, т.е. R Í М₁ ´ М₂. При этом множество М₁ называют областью определения отношения R, множество М₂ - областью значений. Часто рассматривают отношения R между парами элементов одного и того же множества М, тогда R Í М ´ М. Если a, b находятся в отношении R, это часто записывается как а R b.

Пусть R Í А ´ В определено в соответствии с изображением на рис.1. Область определения D(R) и область значении Q(R) определяются соответственно:

D(R) = {а: (а, b) Î R}, Q(R) = {b: (a, b) Î R}.

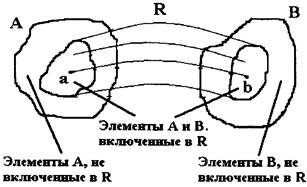
Рис.1

Способы задания бинарных отношений - любые способы задания множеств (так как отношения определены выше как подмножества некоторых множеств - прямых произведений). Отношения, определенные на конечных множествах, обычно задаются:

1.Списком (перечислением) пар, для которых это отношение выполняется.