Решение типового примера

Пример 4(а). Даны векторы , причём , , , = = . Найти угол между векторами и .

Для нахождения угла между векторами и воспользуемся формулой:

.

Найдём . Для этого воспользуемся распределительным свойством:

.

По определению скалярного произведения:

;

.

Найдём .

.

Следовательно,

.

Тогда

.

 

Пример 4(б). Раскрыть скобки и упростить выражение:

.

Сначала найдём векторные произведения, используя то, что

 

.

 

Получим

.

Затем найдём скалярные произведения, используя то, что

.

Получим

.

 

Задача 5. Даны вершины пирамиды . Найти: 1) площадь грани ; 2) объём пирамиды; 3) длину высоты пирамиды, проведённой из вершины .

5.1. , , , ;

5.2. , , , ;

5.3. , , , ;

5.4. , , , ;

5.5. , , , ;

5.6. , , , ;

5.7. , , , ;

5.8. , , , ;

5.9. , , , ;

5.10. , , , ;

5.11. , , , ;

5.12. , , , ;

5.13. , , , ;

5.14. , , , ;

5.15. , , , ;

5.16. , , , ;

5.17. , , , ;

5.18. , , , ;

5.19. , , , ;

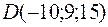5.20. , , , ;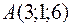

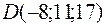5.21. , , , ;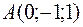

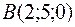5.22. , , , ;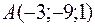

5.23. , , , ;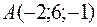

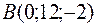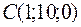5.24. , , , ;

5.25. , , , ;

5.26. , , , ;

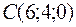5.27. , , , ;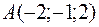

5.28. , , , ;

5.29. , , , ;

5.30. , , , .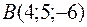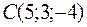