Разложите на множители.

Упростите выражение.

а) -2 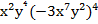; б) (5х-4)(5х+4)- .

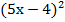РЕШЕНИЕ:

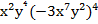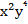а) -2 = -2 ·81х²⁸у⁸ (возвели в степень одночлен) = -162х³⁰у¹²

б) (5х-4)(5х+4)- 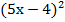=25х²-16-(25х²-40х+16) (воспользовались формулами ФСУ) = 25х²-16-25х²+40х-16 (раскрыли скобки перед которыми стоит знак минус)=40х-32 (привели подобные слагаемые)

Разложите на множители.

а) 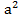в-81в; б) 6 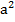-36а+54; в) 2 .

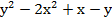РЕШЕНИЕ:

а) 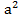в-81в = в(а²-81) (вынесли общий множитель за скобки) = в(а-9)(а+9) (воспользовались формулами ФСУ)

б) 6 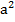-36а+54 = 6 (а²-6а+9) (вынесли общий множитель за скобки) = 6 (а-3)² (воспользовались формулами ФСУ)

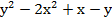в) 2 = (2 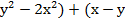) (сгруппировали) = 2( 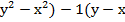) (вынесли общий множитель за скобки) = 2 (у-х)(у+х) - (у-х) (воспользовались формулами ФСУ) = (у-х) (2(у-х)-1) (вынесли общий множитель за скобки) = (у-х) (2у-2х-1)

3. Решите уравнение.

а) 3-4(1-х)=3(3х+1); б) 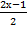- 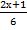=4; в)3 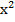+6х=0.

РЕШЕНИЕ:

а) 3-4(1-х)=3(3х+1)

3-4+12х=9х+1 (раскрыли скобки)

12х-9х=1-3+4 (неизвестные собрали в левой части, известные в правой)

3х=2 (привели подобные слагаемые)

х= (разделили обе части уравнения на коэффициент, стоящий перед х)

 

б) 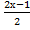- 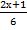=4

3 (2х-1) – (2х+1) = 24 (умножаем обе части уравнения на Наименьший Общий Знаменатель, чтобы избавиться от знака дроби)

6х-3-2х-1=24 (раскрыли скобки)

6х-2х=24+3+1

4х=28

х=7

в)3 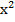+6х=0

3х(х+2)=0 (вынесли общий множитель за скобки)

3х=0 или х+2=0 (произведение равно нулю, если хотя бы один из множителей равен нулю)

х₁=0 или х₂₌ -2

4. Решите систему уравнений

у-2х=7;

7у-5х=4.

РЕШЕНИЕ:

Методом подстановки:

у=7+2х (выразили у из первого уравнения)

7 (7+2х) -5х=4 (подставили у во второе уравнение)

49+14х – 5х =4

9х = -45

х = -5, (теперь подставим х = -5 в выражение) у=7+2·(-5)= -3. Ответ: (-5;-3)

 

5.а) Постройте график функции у=2-5х.

РЕШЕНИЕ: строим график используя всего две точки (т.к. х в первой степени)

х			10 (сразу проверяем точку А с координатами (10,-48)
у		-3	-48

 

б) Определите, проходит ли график функции через точку А (10;-48). – да, смотрим в таблицу

6. За 5 часов по течению реки лодка проходит расстояние в 2 раза больше, чем за 2 часа против течения. Какова собственная скорость лодки, если скорость течения реки 0,5км/ч?

РЕШЕНИЕ: составим таблицу:

	S	V	t
По течению	в 2 р. >	+0,5 км/ч	5ч
Против течения		-0,5 км/ч	2ч

Пусть х – собственная скорость лодки, тогда (х+0,5) – скорость по течению реки, (х-0,5) скорость против течения реки.

(х+0,5)·5=2·2·(х-0,5)

5х-2,5=4х-2

х=0,5 (км/ч) собственная скорость лодки

7. Докажите, что верно равенство. (t+n)(t-n) – k(2t-k) – (t-k+n)(t-k-n)=0.

РЕШЕНИЕ:

(t+n)(t-n) – k(2t-k) – (t-k+n)(t-k-n)=0.

t²-n²-2kt+k²-(t²-kt-nt+-kt+k²+kn+nt-kn-n²) = 0 (воспользовались формулами ФСУ и правилами умножения одночлена на многочлен, многочлена на многочлен)

t²-n²-2kt+k²-t²⁺kt+nt+kt-k²-kn-nt+kn+n² = 0 (привели подобные слагаемые)

0=0