Тема «Векторная алгебра и аналитическая геометрия»

Вариант 1

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Даны две точки Составить уравнение плоскости, проходящей через точку перпендикулярно вектору .
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

Вариант 2

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Составить уравнение плоскости, проходящей через точку параллельно двум векторам
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.


 

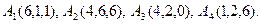
Вариант 3

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Составить уравнение плоскости, проходящей через три точки .
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

 

Вариант 4

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Составить уравнение плоскости, проходящей через точку 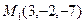параллельно плоскости .
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

 

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

 

Вариант 5

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Составить каноническое уравнение прямой, проходящей через точку перпендикулярно к плоскости
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

 

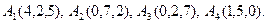
Вариант 6

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Найти угол между прямыми .
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

 

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

Вариант 7

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Найти точку пересечения прямой и плоскости

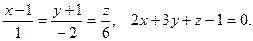
  1. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

 

Вариант 8

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Составить уравнение прямой, проходящей через точку

перпендикулярно к плоскости

  1. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.


Вариант 9

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

 

  1. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой .
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.

 

Вариант 10

  1. Даны три последовательные вершины параллелограмма

Найти:

1) Уравнение стороны

2) Уравнение высоты, опущенной из вершины на сторону , длину этой высоты

3) Уравнение диагонали

4) Площадь параллелограмма

5) Угол между диагоналями параллелограмма.

  1. При каком значении прямая .
  2. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Построить кривую.

  1. Даны координаты вершин пирамиды . Найти уравнение прямой , уравнение плоскости , площадь грани , объём пирамиды.