Характеристики весов

 

К основным характеристикам весов относят устойчивость, чувствитель­ность, постоянство показаний, вариацию показаний и точность измерений.

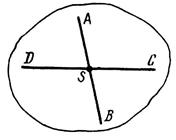
Рис. 2.3. Определение центра тяжести плоского тела

 

Следует отметить, что эти характеристики взаимосвязаны и их можно достигнуть только в результате правильного конструирования весов и их элементов.

 

Устойчивость весов.Характеризует их способ­ность автоматически возвращаться в первона­чальное положение после устранения возмуще­ния, выведшего их из него. Определим условия, характеризующие устойчивость весов. Рассмот­рим неравноплечное коромысло лабораторных весов (рис. 2.4.). Оно будет рычагом первого рода, снабженным передвижной гирей G₁ которое может перемещаться по шкале EF длиной m с нанесенными на

 

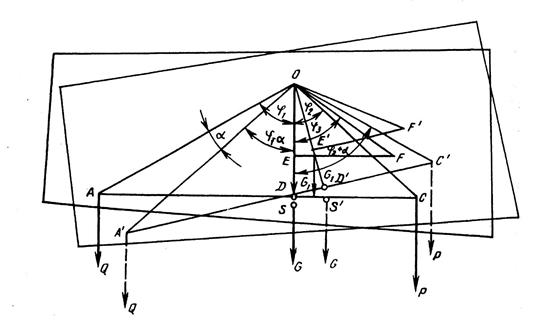
Рис.2.4. Схема к выводу условий устойчивости коромысла

 

ней делениями. В точках А и С, в которых помещены призмы, приложены силы Q и Р, заменяющие силы тяжести гирь и чашек, подвешенных к коромыслу.

Обозначим длины отрезков АО = а; СО = b; SO = s; DO = d; FO = h. Если в начальный момент представить, что чашки с гирями сня­ты, а гиря G₁ перемещена по линейке в точку Е, то коромысло будет находиться в состоянии устойчивого равновесия, так как центры тя­жести коромысла S и гири G₁ расположены ниже точки подвеса. Если теперь к коромыслу приложить силы Р и Q, то для его равновесия необходимо, чтобы выполнялось условие:

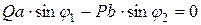(2.4)

Для равновесия коромысла необходимо выполнить соотношение

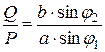
(2.5)

Предположим, что из-за несоответствия плеч сил Р и Q послед­нее условие не выполняется, тогда коромысло повернется на какой-то угол а и займет новое положение, указанное на рисунке 2.4. тонкими линиями. Для этого нового положения уравнение равновесия будет иметь уже несколько другой вид, а именно

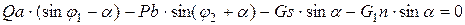(2.6)

где 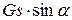— дополнительный момент, возникающий в новом поло­жении коромысла от силы тяжести G; 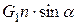— дополнительный мо­мент, возникающий от силы тяжести G₁ гири.

Указанные два момента компенсируют в данном случае несоответ­ствие плеч коромысла.

Вып олнив в выражении (2.6.) некоторые преобразования и считая, что в реальных коромыслах 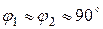, a 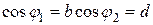по­лучим

 

 

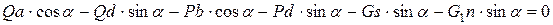
или, группируя члены, окончательно имеем

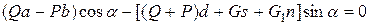(2.7)

Уравнение (2.7) дает условие равновесия коромысла в новом по­ложении, которое оно займет из-за несоответствия плеч. Это равно­весие будет также устойчивым. Для того чтобы определить величину устанавливающего момента, действующего на коромысло, представим мысленно его отклоненным на какой-то угол р. В таком новом по­ложении коромысло не находится в равновесии. Поэтому вместо ра­венства (2.7) получаем неравенство

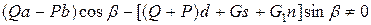(2.8)

которое в левой части аналогично ему, но вместо угла α имеем угол β. Из равенства (2.7) определим член (Qa — Pb) и подставим в не­равенство (2.8) получим

.

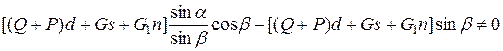Выполнив в последнем выражении некоторые преобразования, окон­чательно будем иметь \

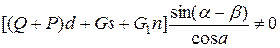(2.9)

Используя выражение (2.9), всегда можно определить величину устанавливающего момента коромысла, если оно каким-либо способом выведено из равновесия. |

Проанализируем полученное неравенство (2.9). Прежде всего отме­тим, что cosα > 0, так как по условиям конструкции угол α < 90°. Поэтому выражение (2.9) не может быть бесконечно большим. Далее представим, что коромысло отклонилось на угол β > а. Для pro чтобы оно возвратилось в исходное положение, т. е. чтобы величина 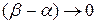, необходимо, чтобы член

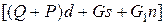>0 (2.10)

так как все выражение (2.9) должно быть отрицательным, а член

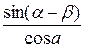как раз имеет знак минус.

Если же коромысло отклонилось на угол β < α, то, для того чтобы оно

возвратилось в исходное положение, выражение (2.9) должно быть

положительным. Это достигается опять же при выполнении условия (2.10), так как член 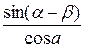в выражении (2.9) в этом случае положителен.

Исходя из этого, можно сделать заключение, что неравенство (2.10) выражает условие устойчивости коромысла. Учитывая его, можно ана­лизировать различные конструкции коромысел с точки зрения пригод­ности их для использования в весах. Заметим, что в неравенстве (2.10) величины сил положительны, а величины d, s, п в зависимости от кон­струкции того или иного коромысла могут иметь различные знаки.

Примем, что при расположении опоры выше точек D, S, Е (рис. 2.4) эти величины положительны, в противном случае — отрицательны. Рас­смотрим, как влияет на устойчивость весов изменение отдельных параметров, входящих в неравенство (2.10). Обычно шкалу, по которой передвигают гирю G₁, располагают так, чтобы центр тяжести гири пере­мещался по горизонтальной линии, проходящей через ось вращения коромысла. В этом случае величина п и член G₁n из выражения (2.10) выпадают. Однако часто рейтерные шкалы помещают на верхнем крае коромысла т. е. выше опоры. В этом случае величина п отрицательна и член Gin также отрицателен. Такое расположение шкал уменьшает устойчивость весов. В зависимости от конструкции коромысла могут быть различные варианты расположения его центра тяжести:

1. Центр тяжести коромысла находится выше опоры. В этом случае коромысло, не нагруженное силами Р и Q, будет в состоянии неустой­чивого равновесия, так как величина s отрицательна. Из неравенства (2.10) следует: для того чтобы нагруженное коромысло находилось в состоянии- устойчивого равновесия, необходимо выполнить условие

.

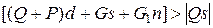Причем коромысло будет тем более устойчивым, чем больше вели­чина d (просвет между призмами) или чем больше силы Р и Q. Для коромысла, имеющего в ненагруженном состоянии неустойчивое равно­весие (величина d имеет отрицательное значение), добиться устойчи­вого равновесия в нагруженном состоянии, как правило, не представ­ляется возможным. Это объясняется тем, что член G₁n мало влияет на устойчивость коромысла.

2. Центр тяжести коромысла совпадает с центром тяжести опоры. Ненагруженное коромысло будет находиться в безразличном равнове­сии. Анализ выражения (2.10) показывает, что коромысло, у которого величина d положительна, в нагруженном состоянии будет находиться в устойчивом равновесии и его можно использовать в весах. Коромысло с отрицательной величиной d или cd = 0 нельзя использовать в весах, так как оно будет находиться в состоянии неустойчивого или безраз­личного равновесия.

3. Центр тяжести коромысла находится ниже точки опоры. В этом случае величина s положительна. Коромысло будет в состоянии устой­чивого равновесия при всех положительных значениях d и в некотором диапазоне отрицательных значений d. Минимальное значение величи­ны d, при котором весы будут находиться в состоянии устойчивого равновесия, определяют из неравенства

.

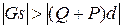Анализ различных по конструкции коромысел и выше проведенный показывают, что на их устойчивость в основном влияет величина s, а ве­личины d и n можно не учитывать из-за малого значения.

 

 

Чувствительность весов. Это отношение углового (или линейного) перемещения показывающего элемента весов к массе груза, вызвавшего это перемещение. Отсюда следует, что чем больше перемещение пока­зывающего элемента весов при одной и той же массе груза, тем они чувствительнее.

return false">ссылка скрыта

Для определения зависимости, характеризующей чувствительность весов, вернемся к уравнению равновесия коромысла, считая, что откло­нение коромысла на угол а вызвано не несоответствием плеч коромысла номинальным размерам, а разностью сил Q — Р на величину р, т. е. Q — р=p. Уравнение равновесия коромысла аналогично уравнению (2.6). Вводя ранее принятые допущения и выполняя такие же преобразования, получим уравнение равновесия коромысла для нашего случая точно такое же, как и уравнение (1.8). Разделив оба члена уравнения на cosα и выполнив преобразования, будем иметь равенство

.

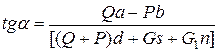Учитывая, что для равноплечего коромысла а = b и что для неболь­ших углов tg a ≈а, получим

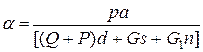
Разделив правую и левую части уравнения на р, окончательно будем иметь выражение для чувствительности весов в виде

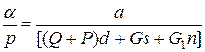
(2.11)

Уравнение (2.11) характеризует чувствительность весов при угловом перемещении стрелки, когда массу груза регистрируют считыванием величины угла отклонения стрелки. Угол а можно заменить его выражением 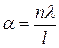где п — число делений, пройденных стрелкой при взвешивании груза; λ — длина одного деления шкалы; l —длина пока­зывающей стрелки, отсчитываемая от ее оси вращения до свободного конца.

Тогда выражение для чувствительности весов можно записать как

 

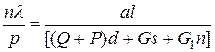(2.12)

Из полученных выражений следует, что чувствительность весов воз­растает с уменьшением сил тяжести коромысла, гири,[взвешиваемого груза, с увеличением плеча коромысла и длины показывающей стрелки.

Проанализируем влияние величин, входящих в уравнение (2.11), на чувствительность весов и выявим из них такие, изменение которых наиболее выгодно для увеличения чувствительности, пусть d = п = 0. Тогда уравнение (2.11) можно упростить

.

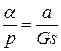Используя полученное выражение, можно определить минимальное значение массы груза, которую будут чувствовать весы, т. е.

,

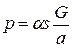а из этого выражения легко видеть, что чувствительность весов тем больше, чем меньше отклонение G/a. Однако известно, что с возраста­нием длины плеча коромысла его масса растет значительно быстрее. Поэтому с увеличением плеча коромысла чувствительность весов будет не возрастать, а, наоборот, уменьшаться.

Необходимо отметить, что в одном случае все же чувствительность прямо пропорциональна длине плеча коромысла. Это будет тогда, когда величина s = 0, т.е. центр тяжести коромысла, совпадает с осью его вращения. Для весов, снабженных таким коромыслом, момент си­лы тяжести его равен нулю, т. е. Gs = 0, и формула чувствитель­ности имеет вид

.

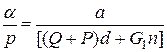Но, как уже было ранее разобрано, коромысло, у которого центр тяжести совпадает с осью вращения, находится в ненагруженном сос­тоянии в безразличном равновесии. Весы с такими коромыслами, какправило, не выпускают.

Чувствительность весов, как следует из уравнения (2.11), в общем случае величина непостоянная и в значительной мере зависит от массы груза, подлежащего взвешиванию. С ее увеличением она уменьшается.

Далее, анализируя уравнение (2.11), можно показать условия, при которых чувствительность весов будет постоянной величиной. Для этогонеобходимо, чтобы величина d = 0, т. е. грузоприемные призмы и опора находились на одной линии. В этом случае величина момента (Q + P)d = 0 и выражение, по которому рассчитывают чувствитель­ность весов, принимает вид

.

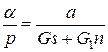Коромысла с указанным призм и опор используют в весах для точного взвешивания.

Кроме рассмотренных выше постоянно действующих факторов на чувствительность весов влияют переменные факторы, обусловленные правильностью монтажа, ремонта и эксплуатации весов. Прежде всего к ним необходимо отнести трение в местах соприкосновения призм и подушек, ориентацию в. пространстве тяг, связывающих рычаги между собой и с коромыслом.

Следует отметить существенное влияние отклонения расположения тяги от вертикального на чувствительность весов. Здесь могут быть два варианта:

1. Тяга коромысла образует с линией, проходящей через острие призм, тупой угол (рис. 2.5а). В этом случае горизонтальная составляющая Р|, возникающая от дейст­вия силы Р в устойчивых коро­мыслах, увеличивает их устойчи­вость, одновременно уменьшая чувствительность,

2. Тяга коромысла образует с линией, проходящей через острие призм, острый угол (рис. 2.5б). В этом случае горизонтальная сос­тавляющая Р₁ силы Р уменьшает устойчивость весов и повышает их чувствительность.

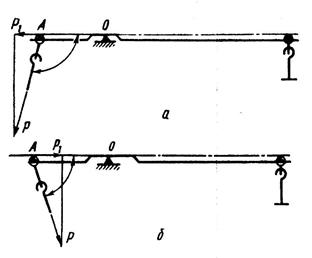
Рис. 2.5. Влияние расположения тяги на чувствительность весов:

а - тяга образует тупой угол с осью коромысла;

б - тяга образует острый угол с осью коромысла;

 

Поэтому в том и другом случаях чувствительность весов изменяется. При возникновении горизонтальных сил, растягиваю­щих подплатформенные рычаги и возникающих из-за отклонения соединительных серег от вертикального положения, наблюдается то же самое.

 

Постоянство показаний весов. Характеризует способность весов за­нимать одно и то же Положение равновесия под действием на них одинаковых по значению нагрузок. Постоянство показании весов отра­жает влияние как систематических, так и случайных погрешностей на результаты взвешивания. Указанное свойство во многом определяет­ся конструктивными особенностями весов, точностью изготовления их элементов и тщательностью сборки.

Весы могут иметь хорошие показатели устойчивости, чувствитель­ности, но если повторные взвешивания одного и того же груза дают различные показания, то они могут быть забракованы. Однако в реаль­ных случаях никогда нельзя добиться точного совпадения результатов многократного взвешивани я, которые зависят от случайных факторов, вызванными случайными погрешностями измерений. Браковать следует те весы, у которых несовпадение результатов многократного взвешива­ния достигает значительных расхождений, выходящих за пределы точности тех или иных весов. С другой стороны, весы тем точнее, чем большим постоянством показаний они обладают.

 

Вариации показаний весов. Это наибольшая разность между повтор­ными показаниями весов, соответствующими одному и тому же значению измеряемой величины в одних и тех же условиях их применения.

 

Точность измерений. Важнейшая характеристика результатов изме­рений, при помощи которой можно оценить возможность использования полученных результатов для тех целей, ради, которых они были прове­дены. Под точностью измерений понимают степень приближения резуль­татов к истинному значению измеряемой величины. Согласно ГОСТ 16263—70 количественно точность измерения может быть выражена обратной величиной модуля относительной погрешности.

Точность весового оборудования характеризуется величиной суммар­ной погрешности, состоящей из погрешностей градуировки, подгонки, переменных погрешностей, вариаций. Погрешности средств измерений, в том числе и весов, определенные при нормальных условиях, называют основными. Используя величины основных погрешностей, средства изме­рений подразделяют по точности.

Для весов введены классы точности, которые определяют в зависи­мости от значений предельно допускаемых основных погрешностей (для краткости их называют просто допускаемыми). Способы обозначения классов точности различны. В весовой технике используют различное обозначение класса точности: в некоторых весах используют порядковые числа, начиная от 1,0 для высшего по точности класса, в других — циф­рами, выражающими приведенную допускаемую погрешность, например класс 0,2, если установлена допускаемая погрешность ±20%.