Дальнейшие расчеты производим в среде MathCad.

Пример решения транспортной задачи при помощи

MathCad

На складах A1, A2, A3 хранится a1=100, a2=200, a3=120 единиц одного того же груза соответственно. Требуется доставить его трем потребителям B1, B2, B3, заказы которых составляют b1=200, b2=110, b3=80 единиц груза. Стоимость перевозки Ci,j единицы груза с i – склада j – ому потребителю указаны в транспортной таблице:

 

	b1=200	b2=110	b3=80
a1=100
a2=200
a3=120

 

Найти минимальную стоимость перевозок.

Для этого, сверх имеющихся n пунктов назначения b₁, b₂, b₃,введём ещё один, фиктивный, пункт назначения b₄, которому припишем фиктивную заявку, равную избытку запасов над заявками. А стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения b₄ будем считать равным нулю. Введением фиктивного пункта назначения B ₄ с его заявкой b ₄ мы сравняли баланс транспортной задачи и теперь его можно решать как обычную транспортную задачу с правильным балансом.

(количество перевезенного груза обозначим символами x1….xn соответственно)

 

	b1 = 200	b2 = 110	b3 = 80	b4 = 30
a1 = 100	4 x1	2 x2	6 x3	0 x4
a2 = 200	7 x5	5 x6	3 x7	0 x8
a3 = 120	1 x9	7 x10	6 x11	0 x12

 

Дальнейшие расчеты производим в среде MathCad.

Задаем начальные значения X.

 

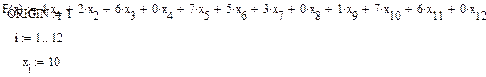
Задаем общую стоимость перевозок:

 

 

Задаем условия:

Используя встроенную функцию Mimimize, находим значения x1…x12 при которых F(x) будет минимальным.

Находим минимальную стоимость перевозки:

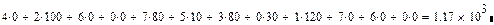
Результаты заносим в транспортную таблицу:

 

	b1=200	b2=110	b3=80
a1=100		2 x2 =100
a2=200	7 x5 = 80	5 x6 = 10	3 x7 = 80
a3=120	1 x9 =120

 

Минимальная стоимость перевозок: F = 1170.