Координаты точки в пространстве.
Пусть в пространстве введена аффинная система координат − ( О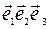 
),
а М – произвольная точка пространства. Вектор 
называется
радиус-вектором точки М. (Рис. 2)
Система векторов , 
является линейно зависимой. Это означает, что вектор можно представить в виде: 
. (1)
Рис. 2
Определение. Коэффициентыx ,y ,zв разложении вектора 
по векторамбазиса данной системы координат называются координатами точки М в системе координат R= (О ).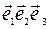
Число х называется абсциссойточки М, у – ординатой, а z – аппликатой точки М. Записывается это следующим образом: М(x,y,z). Другими словами, координатами точки М в системе (О 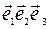) называются координаты её радиус −вектора в базисе данного репера R=(О, 
).
Если аппликата z точки М равна нулю, то из равенства (1) получаем:
= x 
+ y 
.
Векторы , , 
линейно зависимы, поэтому они компланарны. Это означает, что точка М лежит в плоскости Оху. Из предыдущего равенства следует, что в плоскости (Оху) т. М в системе координат (О 
) имеет две координаты М(х,у), а в системе координат (О 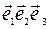) эта точка имеет координаты М(x,y,0). Аналогично, если у=0, то М 
(Оxz) и в системе координат (О 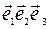) она имеет координаты М(x,0,z), еслих=0, то М (Оxz) => M(0,y,z). Отсюда следует, что если точка М принадлежит оси абсцисс, то у=z=0 то есть в системе координат (О 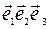) она имеет координаты М(x,0,0), для любой точки оси ординат x=z=0 системе координат (О 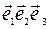) она имеет координаты М(0,у,0), а для любой точки оси аппликат x=y=0 системе координат (О 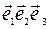) она имеет координаты М(0,0,z).
Для построения т. М(x,y,z) по её координатам в системе О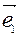 
воспользуемся формулой (1). От начала координат О отложим вектор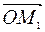 
= =x , затем от т.М1 отложим вектор 
и от точки М2 отложим 
(рис.3)
Рис.3
По правилу многоугольника 
= 
x + y + z . Таким образом, М – искомая точка. Ломаную 
называют координатной ломанной т. М. Итак, для построения точки М достаточно построить её координатную ломанную. Каждое звено имеет длину соответствующей координаты, если единицей измерения есть длина соответствующего базисного вектора.