РАБОТА 6

МОДЕЛИРОВАНИЕ САР С НЕЛИНЕЙНЫМИ СТАТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ В ВИДЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ

Существуют САР с элементами, статические характеристики которых описываются нелинейными аналитическими функцио­нальными зависимостями. Такие нелинейные элементы (см. ниже) линеаризуются на основе ряда Тейлора, в результате чего получа­ется приближенная математическая модель системы в виде струк­турной схемы линеаризованной САР. Примером подобной систе­мы может служить нелинейная САР температуры в инкубацион­ной камере.

В ПК «МВТУ» имеются типовые блоки Функции математиче­ские и Новый, с использованием которых можно моделировать практически любую нелинейную функциональную зависимость. Наличие этих блоков позволяет на основе ПК «МВТУ» моделиро­вать нелинейные САР непосредственно по исходным нелинейным моделям без предварительной линеаризации нелинейных функ­циональных зависимостей, что существенно повышает достовер­ность результатов их исследований.

Цели работы:

• закрепить понятия и вопросы, относящиеся к нелинейным САР (понятия нелинейных элементов и систем, линеаризация нелинейных статических характеристик, понятие линеаризо­ванной системы);

• освоить методику моделирования нелинейных САР на основе ПК «МВТУ» с использованием блоков Функции математтеские и Новый.

Теоретический материал, необходимый для выполнения лабораторной работы.Необходимо владеть понятиями, относящимися к нелинейным системам, а также знать функциональные возможности ПК «МВТУ» и основные этапы работы в его среде. Помимо этого следует изучить порядок и процедуры работы с блоком Новый.

Порядок выполнения работы:

• освоить приемы работы с блоком Новый на базе демонстрационного примера;

• по заданному варианту самостоятельно подготовить исходные данные конкретной САР и выполнить ее компьютерное моде­лирование.

Математическое моделирование технических систем, в том числе САУ и САР, базируется на математических моделях. Под термином математическая модельпонимается записанная в форме математических соотношений совокупность знаний, представле­ний и гипотез о технической системе.

Первичной (исходной) формой представления математической модели (математическим описанием) любой САР является систе­ма дифференциальных и алгебраических уравнений, отображаю­щих динамические свойства объекта регулирования и элементов системы (регулятора). Эти уравнения могут быть определены аналитически на основе законов физики, положенных в ос­нову работы объекта регулирования и элементов системы, или экспериментально с использованием методов активного или пассивного эксперимента.

Аналитический метод определения математических моделей автоматических систем рассмотрим на примере простейшей САР температуры в камере для инкубации яиц (рис. 1.1).

Объектом регулирования в данной САР является инкубацион­ная камера с лотком и яйцами, уложенными на нем. Регулируемая величина — температура в камере U_0к зависит от возмущающего воздействия — температуры окружающей среды Θ₀. Величину Θ_К можно регулировать, изменяя регулирующее воздействие — тем­пературу нагревательного элемента Θ_Н.

Данная САР работает следующим образом. Для измерения тем­пературы в инкубационной камере 7 имеется термопара 2, сигнал которой — ЭДС Е сравнивается с задающим (опорным) сигналом U₀. Изменяя опорное напряжение U₀ с помощью резистора 9, под­ключенного к стабилизированному источнику постоянного тока, задают необходимую температуру в камере инкубатора (Θ_зад = 37,5 ± 0,2 °С). При этом входные и выходные величины элементов САР (ΔU=U₀ - Е; U_y; U_H; Θ _Н) будут иметь определенные значения, соответствующие заданному значению температуры в инкубаторе.

Рис. 1.1. Принципиальная (а) и функциональная (б) схемы САР температуры в камере инкубатора:

1 — инкубационная камера; 2 — термопара; 3 — лоток с яйцами; 4 — нагрева­тельный элемент; 5 — исполнительный орган — тиристорный регулятор напря­жения; 6— силовой блок; 7 — блок управления тиристорами; 8 — электронный усилитель постоянного тока; 9 — задающий резистор; ОР — объект регулирова­ния; РО — регулирующий орган; ИО — исполнительный орган; УО — усилитель­ный орган; СО — сравнивающий орган; ВО — воспринимающий орган

Если, например, внешнее возмущение — температура окру­жающей среды Θ ₀ уменьшилась, то снизится и температура Θ _К внут­ри камеры инкубатора. Это, в свою очередь, приведет к уменьше­нию сигнала термопары Ен к росту сигнала рассогласования ΔU=U₀ - Е, что вызовет увеличение напряжения U_H на нагреватель­ном элементе, выделяемой им мощности Р и его температуры Θ _Н. Увеличение последней приведет к росту температуры Θ _К до задан­ного значения. Увеличение температуры окружающей среды 0о по аналогии с вышеизложенным вызовет обратный эффект (увели­чение Θ _К, Е и уменьшение U_y, U_H, Θ _H).

Рассматриваемая простейшая САР может функционировать только при выполнении условия Θ ₀ < Θ _зад. Если возможны усло­вия, когда Θ ₀ > Θ ₀ (в теплый период года), то САР необходимо дополнить еще одним регулирующим органом, обеспечивающим охлаждение инкубационной камеры.

Задача построения математической модели данной САР состо­ит в определении уравнений, отображающих взаимосвязи в объекте регулирования регулируемой величины Θ_К с входными воз­действиями Θ_Н и Θ ₀, а в остальных элементах системы соответст­венно выходных величин с входными в динамическом режиме.

В динамическом режиме работы любой САР регулируемая ве­личина, а также входные и выходные величины изменяются во времени t. Поэтому все рассмотренные ранее величины примени­тельно к САР (см. рис. 1.1) будут переменными во времени и их следует записывать так: Θ_К(t) , Θ₀(t), Θ_Н(t), Е(t), ΔU(t), Uy(t),U_H(t). Однако для упрощения записи допускается изображение пере­менных величин без указания времени t, что и будет использовано при дальнейшем изложении.

Математическую модель объекта регулирования(камеры инку­батора совместно с лотком и яйцами) определяют на основе урав­нения теплового баланса:

где С_к — усредненная теплоемкость, определяемая теплоемкостями воздуха внутри камеры, яиц и материала лотка; т_к — усредненная масса, определяемая массами воздуха, яиц и лотка; Ф_п.к — поток теплоты, поступающий в камеру от нагрева­тельного элемента; Ф_о.к — поток теплоты, отводимый из камеры через стенки в ок­ружающую среду.

Поток теплоты, поступающий в камеру от нагревателя,

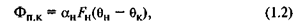
где α_н — коэффициент теплоотдачи нагревательного элемента; F_H — площадь по­верхности нагревательного элемента.

Поток теплоты, отводимый из камеры,

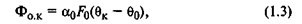
где α₀ — коэффициент теплоотдачи ограждения (стенок) камеры; F₀ — площадь теплоотдающей поверхности стенок камеры.

С учетом формул (1.2) и (1.3) уравнение (1.1) после несложных преобразований примет вид

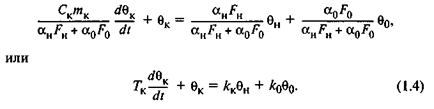
Постоянную времени Т_к камеры и коэффициенты передачи k_н и k_о определяют по формулам

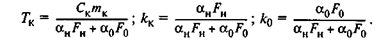
Математическую модель регулирующего органа(нагревательно­го элемента) определяют по аналогии с изложенным ранее на ос­нове уравнения теплового баланса

где С_н, т_н — соответственно удельная теплоемкость и масса нагревательного эле­мента; Р_н — мощность нагревательного элемента.

С учетом формулы (1.2) уравнение (1.5) после соответствую­щих преобразований примет вид

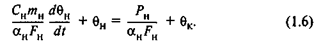
Вводя обозначения

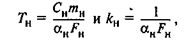
уравнение (1.5) можно окончательно записать так:

где Т_н, k_н — соответственно постоянная времени и коэффициент передачи нагре­вательного элемента.

Мощность

где U_H — напряжение на нагревательном элементе; R— активное сопротивление нагревательного элемента.

Таким образом, динамика нагревательного элемента описыва­ется уравнениями (1.7) и (1.8).

Для получения математической модели(дифференциального уравнения) воспринимающего органа(термопары) запишем урав­нение теплового баланса

где С_т, m_т — соответственно удельная теплоемкость и масса термопары; Θ_Т — тем­пература термопары; Θ_{п т} — поток теплоты, поступающий к термопаре из воздуш­ного пространства камеры.

Поток теплоты

где α_Т — коэффициент теплоотдачи от воздуха к термопаре; F_T — площадь поверх­ности термопары.

С учетом формулы (1.10) уравнение (1.9) примет вид

Вводим обозначение

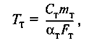
где Т_Т — постоянная времени термопары.

Тогда уравнение теплового баланса окончательно запишем так:

Это уравнение отображает только термический процесс в тер­мопаре. По условию же задачи необходимо определить взаимосвязь температуры в камере Θ_К с ЭДС термопары Е. Зависимость ЭДС термопары от ее температуры Θ_Т можно приближенно описать так:

где k_Т — коэффициент, определяемый по графику градуировочной (статической) характеристики термопары (рис. 1.2) как отношение приращений ΔΕ к ΔΘ в рабо­чей зоне: k_Т = ΔΕ / ΔΘ.

Исключая в уравнениях (1.12) и (1.13) промежуточную пере­менную Θ_Т и учитывая, что

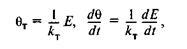
получим окончательно дифференциаль­ное уравнение термопары

 

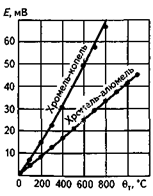
Рис. 1.2. Градуировочные ха­рактеристики термопар

Следует подчеркнуть, что при опре­делении математических моделей инку­бационной камеры, нагревательного элемента и термопары использован один физический принцип (закон) теплотех­ники — принцип теплового баланса. Это обусловлено тем, что работа (физическая суть) инкубационной камеры, нагревателя и термопары ос­нована на тепловых процессах.

Остальные элементы рассматриваемой САР (см. рис. 1.1) — тиристорный регулятор напряжения (ИО) и электронный усилитель (УО) являются электротехническими устройствами. Их математи­ческие модели можно определить на основе законов электротех­ники. Эти элементы относятся к электронным устройствам, в ко­торых входные сигналы передаются на выход практически без ка­ких-либо временных задержек, так как ток в них создается за счет электронов и «дырок», обладающих сверхмалой массой. Поэтому математические модели тиристорного регулятора напряжения (усилителя) и электронного усилителя описываются соответст­венно следующими алгебраическими уравнениями:

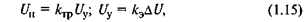
где k_тр, k_э — коэффициенты усиления соответственно тиристорного регулятора и электронного усилителя

Вывод уравнений (1.15), выполненный на основе законов Кирхгофа, можно найти в любом учебнике по электротехнике.

Таким образом, с учетом зависимости ΔU=U₀ - Е, отображаю­щей обратную связь в системе, на основе уравнений (1.4), (1.7), (1.8), (1.14) и (1.15) математическая модель САР температурыв ин­кубаторе может быть представлена следующей системой уравнений:

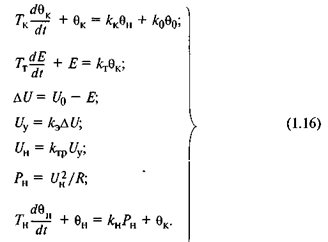
Анализ системы уравнений (1.16) показывает, что рассматри­ваемая САР нелинейная. Ее нелинейность обусловлена наличием нелинейного алгебраического уравнения (1.8). Это уравнение можно привести к линеаризованному виду, используя известные в теории автоматического регулирования методы линеаризации [2], основываясь на следующих рассуждениях.

Рассматриваемая система стабилизации температуры в инку­баторе (см. рис. 1.1) предназначена для поддержания температуры в камере Θ_К на заданном уровне. При работе системы величина 8_К изменяется в пределах малых отклонений ± ΔΘ_К относительно за­данного значения. В пределах малых отклонений будут изменяться также все входные и выходные величины элементов САР, в том числе напряжение U_н на нагревательном элементе и его мощность Р соответственно относительно значений U_н0 и P₀ (здесь U_н0, P₀ — напряжение на нагревательном элементе и его мощность, соответ­ствующие установившемуся заданному значению температуры в инкубаторе).

Для линеаризации уравнения (1.8) воспользуемся аналитическим методом линеаризации, разложив его в ряд Тейлора, при U = U_н0.

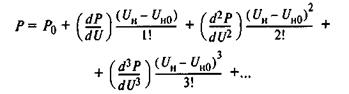
Пренебрегая нелинейными членами ряда ввиду их малости, получаем

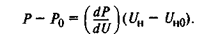
Так как Р – P₀ = ΔР, a U_H - U_н0 = ΔU_H, то линеаризованное уравнение в пределах малых отклонений мощности ΔР и напря­жения ΔU_H можно записать в следующем виде:

Для определения k_p возьмем производную от исходной функ­ции (1.8)

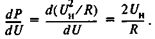
Подставив в это выражение U_H = U_н0, получим

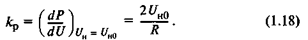
С учетом выражения (1.18) линеаризованное уравнение мощ­ности нагревательного элемента (1.17) примет вид

Таким образом, нелинейную математическую модель САР (1.16) с учетом уравнения (1.17) можно рассматривать как линеа­ризованную математическую модель.

Известно [2...4], что линейные и линеаризованные математи­ческие модели САР в виде дифференциальных и алгебраических уравнений могут быть представлены соответствующими им пере­даточными функциями. Для рассматриваемой САР передаточные функции на основе уравнений (1.4), (1.7), (1.14), (1.15), (1.17) по­сле их преобразования по Лапласу при нулевых начальных усло­виях примут вид:

передаточная функция камеры инкубатора по регулирующему воздействию;

 

- передаточная функция камеры по возмущающему воздействию;

 

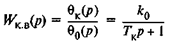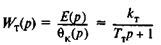— передаточная функция термопары;

 

— передаточная функция нагревателя по каналу мощности Р;

 

— передаточная функция нагревателя по каналу температуры Θ_К;

 

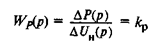- передаточная-.функция, соответствующая линеаризованному уравнению (1.17);

 

- передаточная функция алектринного усилителя;

 

- передаточная функция шристорного регулятора напряжения,

 

где Θ_к(р), Θ_Н(р), Θ₀(р), Е(р), Р(р), ΔР(р), U_H(p), ΔU_H(p), U_y(p), ΔU(p) - изображения по Лапласу соответственно температуры в камере Θ_к, нагревателя Θ_Н, окружающей атмосферы Θ₀, ЭДС Е термопары, мощности Р и ее отклонения ΔР, напряжения U_H и его отклонения ΔU_H, напряжения U_y и сигнала рассогласования ΔU при ну­левых начальных условиях.

Интерпретация математических моделей автоматических сис­тем совокупностью передаточных функций объекта регулирова­ния и элементов регулятора позволяет представить математиче­ские модели САР графически в виде структурных схем [2...4], ко­торые достаточно просто составить на основе заданных функцио­нальных схем и передаточных функций. Применительно к рассматриваемому примеру структурная схема САР (см. рис. 1.1) в соответствии с ее функциональной схемой и приведенными вы­ше передаточными функциями будет иметь вид, показанный на рисунке 1.3. На структурных схемах вместо изображений пере­менных (входных и выходных величин) допускается указывать их оригиналы, что существенно повышает их дидактичность и фи­зическую наглядность.

Если математический аппарат передаточных функций приме­ним только для линейных и линеаризованных САР, то графиче­ские представления динамических свойств автоматических сис­тем с использованием структурных схем можно использовать так­же для любых нелинейных САР. На структурных схемах можно отображать нелинейные зависимости, заданные как аналитиче­ски, так и графически. При графическом представлении нелинейностей в соответствующих звеньях структурных схем указывают эти графики. Если нелинейность задана ввиду функциональных зависимостей, то в звеньях структурных схем указывают соответ­ствующие формулы или адекватные им условные графические обозначения. На рисунке 1.4 в качестве примера показаны струк­турные схемы некоторых нелинейных звеньев и элементов.

На основе изложенного исходную нелинейную математиче­скую модель САР температуры в камере инкубатора (1.16) можно представить в виде структурной схемы (рис. 1.5).

Обобщая изложенное, можно отметить следующее: исходные математические модели САР — это системы дифференциальных и

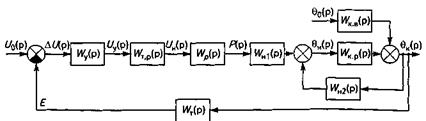
Рис. 1.3. Структурная схема линеаризованной САР температуры в инкубаторе

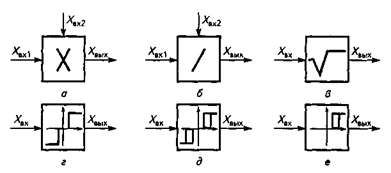
Рис. 1.4. Структурные схемы нелинейных звеньев и элементов:

а — звено, реализующее умножение двух входных величин: х_вых = x_вх1x_вх2; б — звено, реализующее деление одной входной величины на другую (х_вых = x_вх2/x_вх1; в — звено, реализующее извлечение квадратного корня из входной величины (х_вых = = 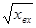); г — трехпозиционный релейный элемент с зоной нечувствительности;д — трехпозиционный элемент с зоной нечувствительности и гистерезисом; е — двухпозиционный элемент с зоной нечувствительности и гистерезисом

алгебраических уравнений, а производные от них — передаточные функции и структурные схемы.

Кроме рассмотренных ранее форм представления математиче­ских моделей в теории автоматических систем используют мате­матические модели в форме Коши и векторно-матричной форме, изучение которых не предусмотрено типовой программой дисци­плины «Автоматика» для агроинженерных специальностей.

В данном учебном пособии использованы математические мо­дели в виде структурных схем, так как в основу ПК «МВТУ», яв­ляющегося его программной базой, заложен метод структурного моделирования. Следует подчеркнуть, что с помощью ПК «МВТУ» можно моделировать также'автоматические системы, представленные в форме Коши и векторно-матричной форме.

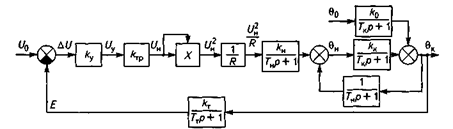
Рис. 1.3. Структурная схема линеаризованной САР температуры в инкубаторе

Рис. 1.4. Структурные схемы нелинейных звеньев и элементов:

а — звено, реализующее умножение двух входных величин: х_вых = x_вх1x_вх2; б — звено, реализующее деление одной входной величины на другую (х_вых = x_вх2/x_вх1; в — звено, реализующее извлечение квадратного корня из входной величины (х_вых = = 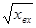); г — трехпозиционный релейный элемент с зоной нечувствительности;д — трехпозиционный элемент с зоной нечувствительности и гистерезисом; е — двухпозиционный элемент с зоной нечувствительности и гистерезисом

алгебраических уравнений, а производные от них — передаточные функции и структурные схемы.

Кроме рассмотренных ранее форм представления математиче­ских моделей в теории автоматических систем используют мате­матические модели в форме Коши и векторно-матричной форме, изучение которых не предусмотрено типовой программой дисци­плины «Автоматика» для агроинженерных специальностей.

В данном учебном пособии использованы математические мо­дели в виде структурных схем, так как в основу ПК «МВТУ», яв­ляющегося его программной базой, заложен метод структурного моделирования. Следует подчеркнуть, что с помощью ПК «МВТУ» можно моделировать также'автоматические системы, представленные в форме Коши и векторно-матричной форме.

Рис. 1.5. Структурная схема нелинейной САР температуры в инкубаторе