Расчет значений функции и плотности экспоненциального распределения

	l
	0,5
X	F(x)	P(x)
		0,5
0,1	0,048771	0,475615
0,2	0,095163	0,452419
0,3	0,139292	0,430354
0,4	0,181269	0,409365
0,5	0,221199	0,3894
0,6	0,259182	0,370409
0,7	0,295312	0,352344
0,8	0,32968	0,33516
0,9	0,362372	0,318814
	0,393469	0,303265

 

 

3. Семейство распределений Вейбулла является двухпараметрическим и описывает положительные случайные величины. Считается, что распределению Вейбулла подчиняются времена безотказной работы многих технических устройств. Если b=1, то распределение Вейбулла превращается в экспоненциальное распределение, а если b=2 - в так называемое распределение Релея.

 

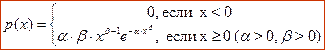
Таблица 2

Расчет значений функции и плотности распределения Вейбулла

	l	b	l	b	l	b	l	b
	0,5	0,5			1,5	1,5
X	F(x)	P(x)	F(x)	P(x)	F(x)	P(x)	F(x)	P(x)
	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000
0,2	0,469	0,840	0,181	0,819	0,048	0,348	0,010	0,099
0,4	0,591	0,457	0,330	0,670	0,129	0,450	0,039	0,192
0,6	0,666	0,305	0,451	0,549	0,224	0,491	0,086	0,274
0,8	0,718	0,223	0,551	0,449	0,323	0,495	0,148	0,341
	0,757	0,172	0,632	0,368	0,420	0,474	0,221	0,389

 

 

4. Другим распределением, также достаточно хорошо описывающим времена безотказной работы различных технических устройств, является гамма-распределение. Время выполнения какой-либо задачи, например обслуживания клиента или ремонт машины

 

Расчеты произвести для a=b=0,5; a=b=1; a=b=1,5; a=b=2.

 

	a	b
	0,5	0,5
X	F(x)	P(x)
0,1	0,472911	2,06576619
0,2	0,628907	1,19593416
0,3	0,726678	0,799471056
0,4	0,794097	0,566858261
0,5	0,842701	0,415107497
0,6	0,878665	0,310249477
0,7	0,905736	0,235168293
0,8	0,926362	0,180104223
0,9	0,94222	0,139023667
	0,9545	0,107981933

 

 

Контрольные вопросы

1. Дать определение функции и плотности непрерывной случайной величины.

2. Каковы свойства плотности непрерывной случайной величины.

3. Описать функцию и плотность нормального распределения.

4. Описать функцию и плотность распределения Вейбулла.

5. Сравнить теоретическую плотность нормального распределения и экспериментальную и объяснить различия в их форме.