Расчет значений функции и плотности нормального распределения

Распределения непрерывных случайных величин

Цель:познакомиться с распределениями непрерывных случайных величин. Сформировать представления о виде функции и плотности непрерывных распределений.

 

Построить функции и плотности для распределений:

· нормального (см. табл.1);

· экспоненциального распределения (см. табл.2);

· Вейбулла с параметрами b и l (см. табл. 3);

· Гамма-распределения.

Плотности для каждого распределения представить на одном графике. Функции для каждого распределения представить на одном графике. Встроенные функции Excel для искомых распределений: нормальное – НОРМРАСП(); экспоненциальное - ЭКСПРАСП(); распределение Вейбулла - ВЕЙБУЛЛ(); гамма-распределение - ГАММАРАСП().

1. В лабораторной работе №1 были получены полигон частот, среднее арифметическое, дисперсия.

· Построить теоретическое распределение нормальной плотности, используя значения (min,max, средне арифметическое, стандартное отклонение) из первой лабораторной работы. Первое значение в выборки взять равным минимальному варианту. Шаг изменения Dx_i — выбрать 2,75. Число значений в выборке n должно быть около 20.

· Сравнить внешний вид полученной кривой с полигоном относительных частот.

Таблица 1

Расчет значений функции и плотности нормального распределения

X		41,75	44,5	47,25	…
F(x)	0,021	0,034	0,054	0,082	…	0,989
P(x)	0,004	0,006	0,009	0,012	…	0,002

 

2. Экспоненциальное распределение используется в тех случаях, когда интервал времени между поступлениями требований в систему, происходящими с постоянной интенсивностью. Функция экспоненциального распределения имеет вид:

 

 

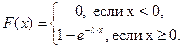Расчеты произвести для l=0,5; l=1; l=1,5; l=2.

Таблица 2