Раздел 5. Общие принципы проверки статистических гипотез
Обычно исследование проводится для проверки гипотезы, которая является следствием теоретических представлений. Эта гипотеза содержит утверждение о связи абстрактных категорий, относящихся к свойствам более или менее широкой совокупности объектов — генеральной совокупности.
Предположение, которое проверяется с применением научного метода, будем называть научной гипотезой.Следует отметить, что не всякая гипотеза, а только та, которая допускает для своей проверки применение научного метода, может претендовать на научность. Кроме того, можно научно проверять гипотезы относительно любых мелких проблем, обладающих ничтожной научной или практической значимостью. Сам факт применения научного метода вовсе не гарантирует, что проверяемая гипотеза представляет научный интерес.
Любое исследование сводится к выявлению связи между переменными. Связь эта может выражаться в величине и направлении различий между сравниваемыми группами или в знаке и величине коэффициента корреляции. То есть связь характеризуется своей силой и направлением. Однако есть еще одна не менее важная характеристика связи — ее надежность, истинность. Надежность связи непосредственно связана с репрезентативностью выборки, с тем, насколько уверенно статистики выборки позволяют судить о соответствующих параметрах генеральной совокупности. Ведь связь, обнаруженная в выборке, интересует исследователя лишь в той мере, в какой она позволяет судить о связи, которая существует в генеральной совокупности.
Надежность связиопределяется тем, насколько вероятно, что обнаруженная в выборке связь будет вновь обнаружена (подтвердится) на другой аналогичной выборке, извлеченной из той же генеральной совокупности.
Статистическая гипотеза— это утверждение относительно неизвестного параметра генеральной совокупности, которое формулируется для проверки надежности связи и которое можно проверить по известным выборочным статистикам — результатам исследования. Обычно выделяют основную (нулевую) и альтернативную статистические гипотезы. Основная (нулевая) гипотеза (Но)— содержит утверждение об отсутствии связи в генеральной совокупности и доступна проверке методами статистического вывода. Альтернативная гипотеза (H1)— принимается при отклонении Но и содержит утверждение о наличии связи. При этом нулевая и альтернативная гипотезы представляют собой, в терминах теории вероятности, полную группу несовместных событий: если верна одна из них, то другая является ложной, и наоборот, отклонение одной из них неизбежно влечет принятие другой.
Статистическая значимость (Significant level, сокращенно Sig.), или р-уровень значимости (p-level), - основной результат проверки статистической гипотезы. Говоря техническим языком, это вероятность получения данного результата выборочного исследования при условии, что на самом деле для генеральной совокупности верна нулевая статистическая гипотеза - то есть связи нет. Иначе говоря, это вероятность того, что обнаруженная связь носит случайный характер, а не является свойством совокупности. Именно статистическая значимость, р-уровень значимости является количественной оценкой надежности связи: чем меньше эта вероятность, тем надежнее связь.
Предположим, при сравнении двух выборочных средних было получено значение уровня статистической значимости р = 0,05. Это значит, что проверка статистической гипотезы о равенстве средних в генеральной совокупности показала, что если она верна, то вероятность случайного появления обнаруженных различий составляет не более 5%. Иначе говоря, если бы две выборки многократно извлекались из одной и той же генеральной совокупности, то в 1 из 20 случаев обнаруживалось бы такое же или большее различие между средними этих выборок. То есть существует 5%-ная вероятность того, что обнаруженные различия носят случайный характер, а не являются свойством совокупности.
В отношении научной гипотезы уровень статистической значимости — это количественный показатель степени недоверия к выводу о наличии связи, вычисленный по результатам выборочной, эмпирической проверки этой гипотезы. Чем меньше значение р-уровня, тем выше статистическая значимость результата исследования, подтверждающего научную гипотезу.
Полезно знать, что влияет на уровень значимости. Уровень значимости при прочих равных условиях выше (значение р-уровня меньше), если:
• величина связи (различия) больше;
• изменчивость признака (признаков) меньше;
• объем выборки (выборок) больше.
Статистический критерий (Statistical Test) — это инструмент определения уровня статистической значимости. Как следует из логики проверки статистических гипотез, в качестве основы для применения статистических критериев используют теоретические распределения, для условия, когда верна нулевая гипотеза. Критерий также подразумевает формулу, позволяющую соотнести эмпирическое значение выборочной статистики с этим теоретическим распределением.
Применяя эту формулу, исследователь вычисляет эмпирическое значение критерия. Полученное эмпирическое значение позволяет определить р-уровенъ — значение вероятности того, что нулевая статистическая гипотеза верна.
Помимо формулы эмпирического значения, критерий задает формулу для определения числа степеней свободы. Число степеней свободы (degrees of freedom — обозначается как df)— это количество возможных направлений изменчивости признака. Как правило, число степеней свободы линейно зависит от объема выборки, от числа признаков или их градаций — чем больше эти показатели, тем больше число степеней свободы. В связи с тем, что для каждого случая определение df имеет свою специфику, сейчас подчеркнем лишь следующее. Каждая формула для расчета эмпирического значения критерия обязательно сопровождается правилом (формулой) для определения числа степеней свободы.
Назначение критерия— проверка статистической гипотезы путем определения р-уровня значимости (вероятности того, что Но верна).
Выбор критерияопределяется проверяемой статистической гипотезой.
Критерий включает в себя:
•формулу расчета эмпирического значения критерия по выборочным статистикам;
•правило (формулу) определения числа степеней свободы;
• теоретическое распределение для данного числа степеней свободы;
• правило соотнесения эмпирического значения критерия с теоретическим распределением для определения вероятности того, что Но верна.
Для проверки статистических гипотез применяются различные критерии.
При этом одному теоретическому распределению могут соответствовать разные формулы критериев — в зависимости от проверяемой статистической гипотезы. Но принцип проверки является общим для всего этого многообразия: вычисленное по формуле эмпирическое значение критерия сопоставляется с теоретическим распределением для заданного числа степеней свободы, что позволяет определить вероятность того, что Но верна.
При обработке данных на компьютере при помощи статистической программы (например, SPSS) исследователю достаточно указать программе, какой критерий (метод, тест) необходимо применить к заданной выборке исходных данных. Далее программа сама вычисляет эмпирическое значение критерия и сопоставляет его с теоретическим распределением. В качестве результата исследователь получает значение р-уровня значимости, наряду с эмпирическим значением критерия и числом степеней свободы.
Когда расчеты производятся вручную, исследователь совершает более сложную последовательность действий для проверки гипотезы, включающую применение специальных таблиц критических значений критерия:
1. Выбор критерия в зависимости от вида исходных данных и статистической гипотезы: теоретического распределения, формул расчета эмпирического значения критерия и числа степеней свободы.
2. Расчет по исходным данным (или по имеющимся статистикам) эмпирического значения критерия и числа степеней свободы.
3. Применение Таблицы критических значений критерия позволяет определить значение р-уровня для данного числа степеней свободы.
Таблица критических значенийсодержит значения (квантили) теоретического распределения, соответствующие наиболее важным — критическим значениям р-уровня (0,1; 0,05; 0,01 и т. д.) для различных чисел степеней свободы. P-уровеиь значимости по вычисленному эмпирическому значению критерия при помощи таких таблиц определяется следующим образом. Для данного числа степеней свободы по таблице определяются ближайшие критические значения и р-уровни, им соответствующие.

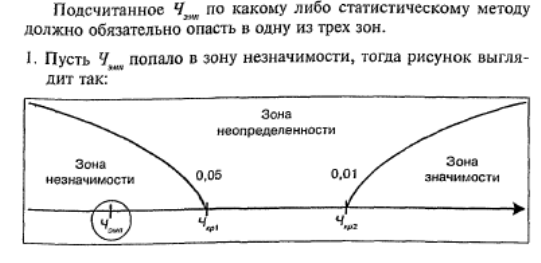
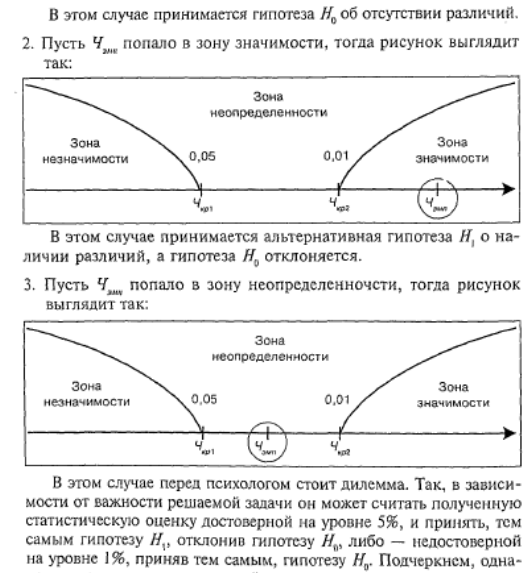


Статистическое решение является основанием для содержательного вывода в отношении проверяемой гипотезы. Но гарантирует ли отклонение Но истинность содержательной гипотезы о наличии связи или различий? Может ли принятие Но служить основанием для вывода об отсутствии связи или различий?
Принятие Но. Из обсуждения оснований принятия статистического решения следует, что, когда принимается Но, всегда остается вероятность того, что связь или различия все же есть. И мы ничего не можем сказать о том, насколько велика или мала эта вероятность.
Принятие Но не означает, что различия отсутствуют или мера связи равна нулю; из этого следует только то, что статистически значимые результаты не обнаружены.
Когда в результате исследования принимается Но, никакого содержательного вывода сделать нельзя. Поэтому выражение «Отрицательный результат исследования — тоже результат» имеет для исследователя исключительно психотерапевтическое значение: отрицательный результат исследования — это отсутствие какого бы то ни было результата!
Отклонение Но. В этом случае остается вероятность того, что Но все-таки верна и эта вероятность равна р-уровню значимости. Следовательно, нельзя утверждать, что результаты доказывают справедливость содержательной гипотезы. Корректным будет более осторожный вывод о том, что получено свидетельство в пользу содержательной гипотезы.





