Теоретические сведения

ЗАДАНИЯ ДЛЯ ЗАНЯТИЯ № 5

«НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ »

 

Теоретические сведения

1. Равномерное распределение на [a, b].

Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

0, при х ≤ а,

f(x) = С, при а< х ≤ b,

0, при х > b.

Найдем С. Так как все возможные значения случайной величины принадлежат интервалу (a, b), то должно выполняться соотношение

= 1 или 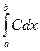= 1, откуда С = 1/(b – a),

Тогда

0, при х ≤ а,

f(x) = 1/(b – a), при а< х ≤ b,

0, при х > b.

Изобразим график f(x) на рисунке .

Найдем F(x).

При х ≤ а F(x) = 0.

При

F(x) = + = = = .

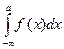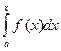При х ≥ b F(x) = 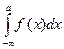+ + = = 1.

Математическое ожидание равномерно распределенной случайной величины есть М(Х) = + + = = = .

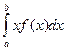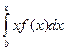То есть математическое ожидание случайной величины, равномерно распределенной на отрезке, есть середина этого отрезка.

Дисперсия случайной величины, равномерно распределенной на отрезке, определяется так:

D(X) = – (М(Х))² = .