А. Законы распределения непрерывных случайных величин.

ЗАДАЧИ К ЭКЗАМЕНУ

ФЭУБ, 2 КУРС 3 СЕМЕСТР

1. ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ.

А. Законы распределения непрерывных случайных величин.

1. Найти F(X), M(X), D(X).

 

2. Найти F(X), M(X), D(X).

 

3. Найти F(X), M(X), D(X).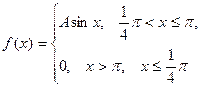

4. Найти F(X), M(X), D(X).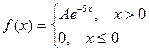

 

5. Найти F(X), M(X), D(X).

 

6. Найти F(X), M(X), D(X).

 

7. Найти F(X), M(X), D(X).

 

8. Найти F(X), M(X), D(X).

 

9. Найти F(X), M(X), D(X).

10. Функция распределения непрерывной случайной величины Х имеет вид:

Найти коэффициент а, плотность распределения f(x), вероятность попадания случайной величины Х в интервал от 0,25 до 0,5.

11. Случайная величина Х задана дифференциальной функцией распределения f(x)=2x в интервале (0;1); вне этого интервала f(x)=0. Найти математическое ожидание и дисперсию величины Х.

12. Известно, что средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратическое отклонение расхода равно 5 кг. Считая расход удобрений нормально распределенной случайной величиной, определить:

1) диапазон, в который вносимая доза удобрений попадает с вероятностью 0,98;

2) вероятность того, что на каждый из 6 га пашни будет израсходовано более 85 кг удобрений.

 

13. Паром для перевозки автомашин через залив подходит к причалу через каждые 2 часа. Считая, что время прибытия автомобилей к парому распределено равномерно, определить:

1) вероятность того, что время ожидания прихода парома будет менее 45 минут;

2) среднее время ожидания автомобилем прихода парома.

 

14. Минутная стрелка часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данный момент часы показывают время, отличающееся от истинного на 20 секунд. Найти среднюю ошибку в определении времени по этим часам.

 

15. Математическое ожидание количества сыра, используемого для изготовления 100 бутербродов, равно 1 кг. Известно, что с вероятностью 0,96 расход сыра на изготовление 100 бутербродов составляет от 900 до 1100 г. Определить, считая расход сыра нормально распределенной сл/величиной:

1) дисперсию расхода сыра на 100 бутербродов;

2) вероятность того, что на каждую из 2 партий по 100 бутербродов уйдет менее 900 г сыра.

 

16. На перекрестке стоит светофор, в котором 1 минуту горит зеленый свет и 0,5 минут – красный. Автомобиль подъезжает к перекрестку в случайный момент времени, не связанный с работой светофора (т.е. можно считать время, прошедшее от момента включения красного сигнала светофора до прибытия автомобиля, распределенным равномерно). Найти:

1) вероятность того, что автомобиль проедет перекресток без остановки ;

2) автомобиль будет ожидать возможности продолжить движение более 0,2 минут.

 

17. Завод изготовляет шарики для подшипников. Номинальный диаметр шариков – 5 мм. Вследствие неточности изготовления шарика фактический его диаметр – случайная величина, распределенная нормально. Среднее квадратическое отклонение равно 0,05 мм. При контроле бракуются шарики, диаметр которых отличается от номинального более, чем на 0,1 мм. Определить:

1) какой процент шариков в среднем будет отбраковываться;

2) вероятность того, что у трех наудачу взятых шариков диаметр будет отличаться от номинального менее, чем на 0,07 мм.

 

18. Поезда данного маршрута городского трамвая идут с интервалом в 3 минуты. Пассажир подходит к остановке в произвольный момент времени. Какова вероятность появления пассажира не ранее, чем через минуту после ухода предыдущего поезда и не позднее, чем за 2 минуты до следующего. Найти среднее время ожидания прихода очередного трамвая.

 

19. Масса вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием 65 т. и средним квадратическим отклонением 0,9. Найти вероятность того, что очередной вагон имеет массу не более 70 т. и не менее 60 т. Определить, в каких границах заключена масса вагона, если известно, что вероятность не выйти за эти границы равна 0, 95.