Испытания Бернулли.

Глава 4. Повторные независимые испытания. Теорема Бернулли.

Теория вероятностей имеет дело с такими экспериментами, которые можно повторять, по крайней мере теоретически, неограниченное число раз. Пусть некоторый эксперимент повторяется n раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений часто называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:

1) результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей»;

2) вероятность «успеха» в каждом последующем испытании не зависит от результатов предыдущих испытаний.

Теорема Бернулли.Если производится серия из n независимых испытаний Бернулли, в каждом из которых успех появляется с вероятностью р, то вероятность того, что успех в n испытаниях появится ровно m раз , выражается формулой

P_n(m)=C_n^mp^mq^n-m, где q=1-p – где вероятность неудачи.

 

Эта формула называется формулой Бернулли.

Задача 1. Игральная кость бросается 6 раз. Найти вероятность того, что ровно 3 раза выпадет «шестерка».

Решение. Пятикратное бросание кости можно рассматривать как последовательность независимых испытаний с вероятностью успеха («шестерки») равно 1/6 и вероятностью неудачи — 5/6. Искомую вероятность найдем по формуле .

Задача 2. Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2 раза.

Решение. Искомая вероятность равна сумме трех вероятностей

Р = Р₆(0) + Р₆(1) + Р₆(2) = 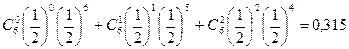.