Эквивалентность процентных ставок различного типа
Продолжим детальное изучение методов определения процентных денег, составляющих сущность большинства финансовых расчетов.
Эквивалентные процентные ставки 
— это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые результаты.
Обозначения, использованные ранее:
i — простая годовая ставка ссудного процента;
d — простая годовая учетная ставка;
ic — сложная годовая ставка ссудного процента;
dc — сложная годовая учетная ставка.
Приравнивая попарно формулы для определения наращенной суммы, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.
Приравнивая соотношения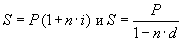 
, получим:
· простая годовая ставка ссудного процента :
; (3.1)
· простая годовая учетная ставка :
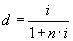. (3.2)
Пример 3.1
Срок уплаты по долговому обязательству — полгода, учетная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?
Решение.
Используем формулу простой годовой ставки ссудного процента (3.1):
.
Пример 3.2
Кредит выдан на полгода по простой ставке ссудного процента 19,8% годовых. Какова доходность данной операции, приемлемой в виде простой учетной ставки?
Решение.
Используем формулу простой учетной ставки (3.2):
.
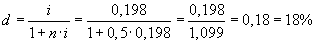Из формул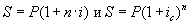 
можем получить эквивалентные ставки простой и сложной годовой ставки ссудного процента:
· простая годовая ставка ссудного процента :
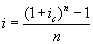; (3.3)
· сложная годовая ставка ссудного процента :
. (3.4)
Пример 3.3
Первоначальная сумма 300000 руб. вложена на 2 года с использованием сложной годовой ставки ссудных процентов в размере 16%. Определите эквивалентную простую годовую ставку ссудных процентов.
Решение.
Используем формулу (3.3):
.
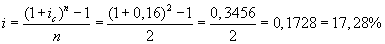Пример 3.4
Сумма 300000 руб. вложена на 2 года с использованием простой годовой ставки ссудных процентов в размере 17,28%. Определите эквивалентную сложную ставку ссудных процентов.
Решение.
Используем формулу (3.4):
.
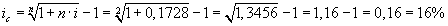Результаты расчетов в примерах 3.3 и 3.4 подтверждают правильность использования формул.
Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы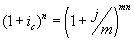 
:
· сложная годовая ставка ссудного процента :
; (3.5)
· номинальная ставка ссудного процента :
. (3.6)
Полученная сложная годовая ставка ссудного процента (ic ), эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов .
3.2.