КУРСК 2004
Для машиностроительных специальностей.
Составитель: И. В. Савенкова
УДК 540
Диаграммы фазовых равновесий. Сплавы: Методические указания к самостоятельной работе студентов машиностроительных специальностей./Курск.гос.техн.ун-т; Сост.: И.В.Савенкова Курск, 2004, с.19.
Содержатся краткие теоретические сведения по фазовым равновесиям, рассматриваются диаграммы сплавов разных видов, приводятся примеры решения задач, на основе анализа диаграмм плавкости..
Табл.1 Библиогр.4:
Рецензент канд. хим. наук, доцент кафедры химии Л.А. Егельская
Текст печатается в авторской редакции.
ЛР №020280 от 09.12.96. ПЛД№50-25 от 01.04.97.
Подписано в печать Формат 60х84 1/16. Печать офсетная.
Усл.печ. Тираж 50 экз.
Курский государственный технический университет.
Подразделение оперативной полиграфии Курского государственного технического университета.
Адрес университета и подразделения оперативной полиграфии: 305040, Курск, ул.50 лет Октября, 94.
ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ
1. Понятие о фазовых переходах.
2. Правило фаз Гиббса – Коновалова. Физический смысл величин, входящих в формулу (понятие о независимом компоненте, фазе, степени свободы, внешних факторах).
3. Классификация систем на основе правила фаз (по числу компонентов, по числу фаз, по числу степеней свободы).
4. Понятие диаграммы фазовых переходов (диаграммы состояния).
5. Особенности строения диаграмм состояния при различном типе взаимодействия компонентов системы:
а) диаграммы состояния систем с неограниченной растворимостью компонентов в жидком и твердом состоянии;
б) диаграммы состояния систем с эвтектической смесью компонентов в твердом состоянии;
в) диаграммы состояния систем с химическим (интерметаллическим) соединением.
6. Правило фаз Гиббса в приложении к двухкомпонентным системам:
а) вариантность процессов охлаждения жидкого и твердого металла, сплава;
б) вариантность процессов кристаллизации чистого металла, эвтектического и квазиэвтектического сплава, твердого раствора, химического соединения.
7. Сущность метода термического анализа и его применение для регистрации температур фазовых превращений в сплавах:
а) вид кривых охлаждения чистого металла, химического соединения, эвтектического и квазиэвтектического сплава, твердого раствора;
б) построение диаграмм состояния с помощью кривых охлаждения.
8. Основные линии и точки диаграммы состояния: понятие точки ликвидус и солидус, линии ликвидус и солидус, фазовой области;
9. Определение фазового и компонентного состава по диаграмме состояния.
10. Расчеты по определению состава сплава по диаграммам состояния.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Коровин Н.В. Общая химия. М.: Высшая школа, 1998.
2. Угай Я.А. Общая и неорганическая химия. М.: Высшая школа, 1997.
3. Фролов В.В. Химия. М.: Высшая школа, 1979.
4. Лучинский Г.П. Курс химии. М.: Высшая школа, 1985.
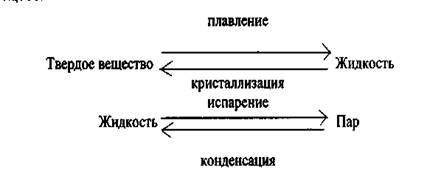
Фазовое равновесие – равновесие перехода вещества из одной фазы в другую без изменения химического состава.
|
Фазовое равновесие- это динамическое равновесие, т.е. скорость прямой реакции равна скорости обратной реакции, а ΔG = 0. Как и для химического равновесия соблюдается принцип Ле Шателье. Следовательно, при повышении температуры фазовое равновесие смещается в сторону эндотермических процессов (плавления и испарения).
Наиболее общим законом гетерогенного равновесия (и химического, и фазового) является правило фаз Гиббса-Коновалова.
С + Ф = К + n, (1)
где К - число независимых компонентов.
Компонентом называется химически однородная составная часть вещества, которая может быть выделена из системы. Например, смесь азота и кислорода состоит из двух компонентов ( O2 и N2), а водный раствор NaCl и KCl– из трех компонентов(NaCl, KCl и H2O).
При фазовом равновесии число независимых компонентов равно общему числу компонентов. При химическом равновесии число независимых компонентов равно общему числу компонентов за вычетом числа химических реакций, связывающих эти компоненты.
ПРИМЕР 1: С(тв) + СО2(г) = 2СО(г).
Система состоит из трех компонентов и двух независимых компонентов, так как один из компонентов можно определить по данной реакции (К=2).
n –число внешних факторов, влияющих на равновесие системы.
Чаще всего – это давление и температура. При этом n = 2, и правило фаз принимает следующий вид:
С + Ф = К + 2 (2)
Ф – число фаз, которое определяется строением системы.
Фаза – это часть системы, однородная во всех её точках по химическому составу и свойствам и отделенная от других фаз системы поверхностью раздела.
Фазы в гетерогенной системе могут представлять собой чистые вещества или иметь переменный состав (растворы или газовые смеси).
ПРИМЕР 2: Н2О(лед) ↔ Н2О(жид)
В этой системе две фазы – твердая и жидкая, т.е. Ф=2
С – число степеней свободы.
Число степеней свободы равно числу внешних факторов (температура, давление, концентрация), произвольное изменение которых в известных пределах не меняет числа и вида фаз. Число степеней свободы характеризует так называемую вариантность системы.
1) Системы, не имеющие ни одной степени свободы (С=0), называются инвариантными или безвариантными. Такие системы могут существовать только при строго определенных условиях (температуре, давлении и концентрации). Изменение хотя бы одного из этих условий ведет к смещению равновесия и исчезновению по крайней мере одной из фаз.
ПРИМЕР 3: Н2О(лед) ↔ Н2О(ж) ↔ Н2О(пар)
В этой системе К=1, Ф=3, следовательно С= К – Ф + 2 = 1 – 3 + 2 = 0.
Система существует только при строго определенных значениях давления и температуры.
2) Системы, обладающие одной степенью свободы, называются моновариантными или одновариантными. В таких системах можно изменять произвольно в некоторых пределах одно из условий, определяющих состояние системы (температуру, давление или концентрацию), не вызывая этим изменения числа или вида фаз системы.
ПРИМЕР 4: Н2О(ж) ↔ Н2О(пар)
Для данной системы К=1, Ф=2, следовательно С = К – Ф + 2
= 1 – 2 + 2 = 1
3) Системы с двумя степенями свободы называются дивариантными или двухвариантными. В таких системах можно произвольно изменять в определенных пределах два из указанных выше условий.
ПРИМЕР 5: С(тв) + СО2(г) = 2СО(г)
В этой системе Ф=2, К=3-1=2, следовательно С К + 2 – Ф =
2 + 2 – 2 = 2.
Могут также существовать системы и с большим числом степеней свободы (поливариантные или многовариантные системы).
При изучении фазовых равновесий широко используется графический метод. Диаграммы называются фазовымидиаграммами, или диаграммами состояния.
Анализ диаграмм состояния позволяет определить число фаз, границы их существования, характер взаимодействия компонентов, наличие вновь образующихся соединений и их состав. Диаграммы позволяют проводить анализ системы без выделения индивидуальных компонентов.
Диаграммы состояния для различных систем строят с помощью метода термического анализа, который является составной частью физико-химического анализа.
Термическим анализом называется такой анализ, который позволяет по характеру изменения температуры в зависимости от времени делать заключения о фазовых изменениях в системе при ее охлаждении.
В основе термического анализа лежит наблюдение за скоростью охлаждения расплавленных чистых веществ и их расплавов различного состава. Термический анализ широко используется в машиностроении для изучения сплавов: их состава и свойств.
Металлические сплавы – это вещества, обладающие металлическими свойствами и состоящие из двух или более элементов, из которых хотя бы один является металлом.
Чтобы построить диаграммы плавкости, вначале получают кривые охлаждения сплавов. Для этого приготавливают ряд сплавов различного состава. Каждый сплав в отдельности расплавляют и записывают кривые охлаждения при помощи термографа, который регистрирует изменение температуры во времени, т. е. кривые охлаждения строятся в координатах время – температура.
ПРИМЕР 6:
| № сплава | ||||||
| Компонент А (в %) | ||||||
| Компонент В (в %) |

|
Рис. 1. Построение диаграммы плавкости по кривым охлаждения.
Кривые охлаждения данных сплавов показаны на рисунке 1.
Для сплавов 1 и 6 получаем кривые охлаждения чистых веществ А и В. Горизонтальная площадка на кривых соответствует кристаллизации данного вещества при его температуре плавления.
Кривые охлаждения остальных сплавов имеют более сложный вид. На них различают участки различной крутизны, которые ограничены друг от друга или точкой перегиба, или горизонтальными участками (плато). Температура начала кристаллизации любого сплава ниже температуры кристаллизации чистого вещества, находящегося в сплаве в избытке. Изменение крутизны кривых охлаждения вызвано нарастанием вязкости сплавов в процессе фазовых превращений: ж ® ж + тв. ® тв. Вследствие этого замедляются диффузионные процессы, ответственные за теплообмен, что ведет к снижению скорости охлаждения сплавов. Таким образом, с понижением температуры участки кривых охлаждения становятся все более пологими. При расчете числа степеней свободы (вариантности) процесса охлаждения пастообразного сплава (кривые охлаждения 2, 3, 5 на рис. 1) важно правильно определить число фаз системы. Жидкий расплав, как правило, представляет собой одну фазу, а кристаллы твердого раствора могут состоять из нескольких твердых фаз.
Используя правило фаз (2) рассчитаем число степеней свободы для данных сплавов, находящихся в пастообразном состоянии:
а) для сплавов 2 и 3: С = 2 + 1 – 2 = 1, т.к. К=2 (сплав состоит из двух компонентов А и В), Ф=2 (сплав состоит из двух фаз Ж + Атв);
б) для сплава 5: С = 2 + 1 – 2 = 1, т.к. К=2, Ф=2 (сплав состоит из двух фаз Ж + Втв);
При самой низкой температуре плавления начинается сплошная кристаллизация расплава, чему соответствуют горизонтальные участки на кривых охлаждения.
Система, создающая условия сплошной кристаллизации (при минимальной температуре плавления), называетсяэвтектикой, а температура и состав, определяющие условия её существования, называются эвтектическими.
Сплав 4, который соответствует эвтектическому составу, кристаллизуется как чистое вещество и образует горизонтальную площадку при температуре эвтектики.
Для данного сплава (в точке эвтектики) С = 2 + 1 – 3 = 0, т.к. К=2, Ф=3 (сплав состоит из трех фаз: Ж + Атв(Е) + Втв(Е), т.е. кристаллы компонентов А и В образуют твердую эвтектику).
Диаграммы плавкости строятся в координатах: состав (ось абсцисс) – температура (ось ординат). На оси состава (см. рис.1) откладывается содержание одного из компонентов сплава (допустим, В) в массовых или атомных процентах от 0% (образец из чистого компонента А) до 100% (образец из чистого компонента В). Содержание второго компонента (в нашем случае компонента А) определяется в любой точке оси состава по разности: 100% минус содержание компонента В. На ординатах температур каждого образца (№1-6) откладывают точки ликвидус (при построении диаграмм плавкости), точки ликвидус и солидус (при построении диаграмм состояния). Далее полученные одноименные точки соединяют соответственно в линию ликвидус и линию солидус.
Линия ликвидус - показывает зависимость температур конца плавления образцов от их состава. Точка ликвидус – соответствует температуре конца плавления (или начала кристаллизации).
Линия солидус - показывает зависимость температур начала плавления образцов от их состава. Точка солидус –соответствует температуре начала плавления (или конца кристаллизации).
Как видно из рис 1, кривая ликвидус состоит из двух ниспадающих ветвей, сходящихся в одной точке, которая является точкой минимума на этой кривой. Точки ликвидус всех сплавов этой системы лежат ниже температур плавления чистых компонентов А и В. Такой вид линии ликвидус характерен для случая эвтектического взаимодействия компонентов системы.
В процессе кристаллизации жидкого сплава металлы ведут себя по – разному, что зависит от радиусов атомов металлов, их типа кристаллической решетки и электрохимических характеристик. Можно выделить три основных случая: