Метод множителей Лагранжа.
Глава 5. Нелинейное программирование
Постановка классической задачи математического программирования.
Цель F x1,x2,…,xn факторы (переменные) инструментальные F ( x1,x2,…,xn )
g1( x1,x2,…,xn ) £ b1,…, gm( x1,x2,…,xn ) £ bm технологические функции ограничений, константы
План, допустимое множество Оптимальный план
Векторная запись F(x) ® max, g(x) £ b, x ³ 0Точка глобального максимума
Оптимальных планов может быть 0, 1, 2, …, ¥
Классическая задача математического программирования F(x) ® max, g(x) = b
Порядок нахождения локального экстремума.
Экстремум во внутренней точке области планов – локальный экстремум
grad F(x) = ÑF = F¢ = 0 в точке локального экстремума – необходимое условие
Матрица Гессе 
Угловой минор матрицы Мк
Пусть F(x*) = 0. Составляют матрицу Гессе и вычисляют ее в т. x* .
У этой матрицы находят миноры M1, M2, …, Mn
Если все Mi > 0, то x* - точка локального минимума,
если же M1 < 0, M2 > 0, … , M2k-1 < 0, M2k > 0, … , то x* - точка локального максимума.
Метод множителей Лагранжа.
Классическая задача, m < n . Если n = 2 , m = 1 , то F(x1, x2) ® max, g( x1, x2) = b Þ x2 = x2(x1)
Необходимое условие экстремума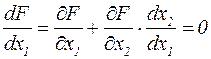 
Из ограничения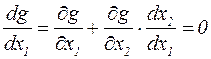 
Вспомогательная переменная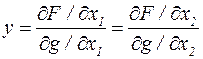 
Þ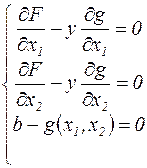 
Функция Лагранжа L(x1, x2, y) = F(x1, x2) + y.(b – g(x1, x2)). В стационарной точке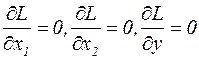 
В общем случае L(x1, x2, …,xn, y1, y2,…, ym) = F(x1, …,xn) + y1 (b1 – g(x1, …, xn)) +…+ ym (bm – g(x1, …,xn)) = F(x) + y·(b – g(x)) множители Лагранжа
Достаточные условия. Матрица Гессе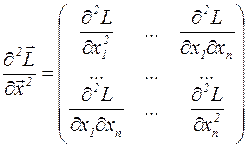 
, матрица Якоби 
Окаймленная матрица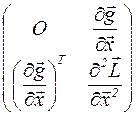 
(m + n) x (m + n)
Локальный минимум, если последние n – m угловых миноров положительны,
локальный максимум, если их знаки чередуются, причем знак наименьшего из них (-1) m + 1